Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

Итак, пусть x ≥ 0. Рассмотрим два случая: | y | ≤ x и | y | > x .

1. x ≥ 0, | y | ≤ x , т. е. − x ≤ y ≤ x . Тогда x ² − y ² ≥ 0 и 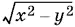— неотрицательное действительное число. Кроме того 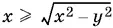и равенство примет вид

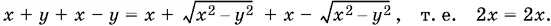
2. x ≥ 0, | y | > x , т. е. y < − x или y > x . Левая часть равенства в этом случае равна 2| y | (случаи y < − x и y > x разберите самостоятельно). Так как | y | > x , то 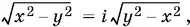следовательно,

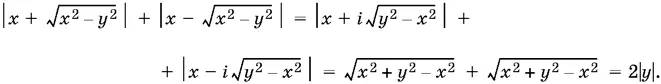
Тем самым доказательство тождества закончено.

7.12.Так как обе части равенства неотрицательны, то можно каждую из них возвести в квадрат

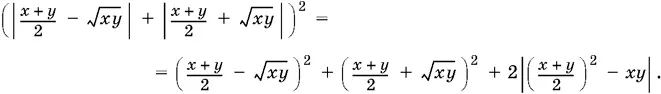
Осуществим действия, указанные в скобках, и заметим, что ( x + y / 2)² ≥ xy . Получим

x ² + 2 ху + y ².

Если возвести в квадрат правую часть, то получим

x ² + 2| ху | + y ².

Так как по условию ху = | ху |, то равенство доказано.

7.13.Возведем выражение

a ⅓+ b ⅓= − c ⅓ (1)

в куб. Получим

a + b + 3 a ⅓ b ⅓( a ⅓+ b ⅓) = − c . (2)

Подставим (1) в (2):

a + b − 3 a ⅓ b ⅓ c ⅓= − c .

т. е.

a + b + c = 3 a ⅓ b ⅓ c ⅓,

или

( а + b + с )³ = 27 аbс .

7.14.По условию

24 х ² + 48 х + 26 = ( ax + b )³ − ( cx + d )³,

т. е. коэффициенты многочленов слева и справа равны. Прежде чем преобразовать правую часть, заметим, что коэффициент при x ³ равен нулю, т. е. а ³ − с ³ = 0, или а = с . Тогда получим, что

( ax + b )³ − ( ax + d )³ = 3 а ²( b − d ) x ² + 3 а ( b ² − d ²) x + b ³ − d ³.

Следовательно,

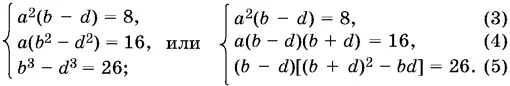
Из (3): b − d = 8/ a ². Из (4) с учетом (3): b + d = 2 а .

Далее найдем:

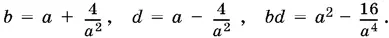
Подставим выражения для b − d , b + d и bd в (5):

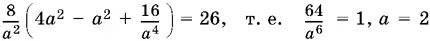
(так как а > 0).

Соответственно, b = 3, d = 1.

Ответ. 2 x + 3; 2 x + 1.

8.1.Положив x − 5 = y , приведем уравнение к виду

( y + ½) 4+ ( y − ½) 4= 1, или (2 у + 1) 4+ (2 у − 1) 4= 16,

откуда после простых преобразований получим

16 y 4+ 24 y 2− 7 = 0.

Ответ. x 1,2= 5 ± i √7/ 2; x 3= 4,5; x 4= 5,5.

8.2.Перемножим попарно первую и третью скобки и две оставшиеся:

(12 х ² + 11 х + 2)(12 х ² + 11 х − 1) = 4.

Обозначив 12 х ² + 11 х + ½ = y , получим

( y + 3/ 2)( y − 3/ 2) = 4,

откуда

y 1= − 5/ 2, у 2= 5/ 2.

Остается решить два квадратных уравнения.

Ответ.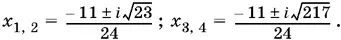

8.3.Запишем уравнение в виде

x ² − 17 = 3 y ²

и рассмотрим случаи x = 3 k , x = 3 k ± 1. B первом случае левая часть примет вид 9 k ² − 17 и не будет делиться на три. B остальных двух случаях в левой части получим

9 k ² ± 6 k − 16,

что снова не делится на три. Поскольку правая часть всегда делится на три, то уравнение не имеет целых решений.

8.4.Решим уравнение относительно x :

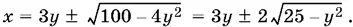
Так как уравнение имеет действительные корни лишь при

25 − y ² ≥ 0, т. е. | y | ≤ 5,

то остается перебрать все целые значения y , для которых 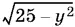— целое число: y = 0, y = ±3, y = ±4, y = ±5. Для каждого значения y найдем два значения x .

Ответ.(10, 0), (−10, 0); (−1, −3), (−17, −3); (1, 3), (17, 3); (−6, −4), (−18, −4); (6, 4), (18, 4); (−15, −5), (15, 5).

8.5.По определению деления имеем тождество

x 99+ x ³ + 10 х + 5 = Q ( x ) ( x ² + 1) + ax + b ,

которое справедливо всюду в области комплексных чисел. Так как частное Q ( x ) нам неизвестно и оно нас не интересует, то в качестве значения x нужно выбрать один из корней выражения x ² + 1, например x = i . Подставив x = i , получим

i 99+ i ³ + 10 i + 5 = аi + b , т. е. 8 i + 5 = аi + b ,

откуда а = 8, b = 5.

Ответ.8 х + 5.

8.6.Перепишем уравнение в виде

y ² 2 x ² + 1/ x ² + 2= 6.

Если x ² ≥ 1, то 2 x ² + 1/ x ² + 2≥ 1.

Так как x = 0 не является целочисленным решением уравнения, то можно утверждать, что y ² ≤ 6. Остается рассмотреть случаи: y ² = 0, y ² = 1, y ² = 4. Первый и второй не приводят к действительным значениям x . Для y ² = 4 находим x ² = 4.

Ответ.(2, 2), (2, −2); (−2, 2), (−2, −2).

8.7.Подставим в данное уравнение x = √3 + 1. После простых вычислений и преобразований получим

36 + 10 а + 4 b + (22 + 6 а + 2 b )√3 = 0.

Сумма двух чисел, из которых одно рациональное, а другое иррациональное, может равняться нулю, только если оба числа равны нулю:

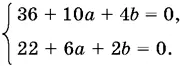
(1).

Решая эту систему, найдем а = −4, b = 1. Поскольку уравнение

x 4− 4 x ³ + x ² + 6 x + 2 = 0

одним из своих корней имеет число √3 + 1, а все коэффициенты уравнения — целые, то следует ожидать, что наряду с этим корнем должен существовать и корень √3 − 1. Подставим это значение x в уравнение и соберем отдельно рациональные и иррациональные члены. Получим

36 + 10 а + 4 b − (22 + 6 а + 2 b )√3 = 0,