Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

x 4− x ² − 2 x − 1 = (1 + x − x ²)(− x ² − x − 1).

Таким образом,

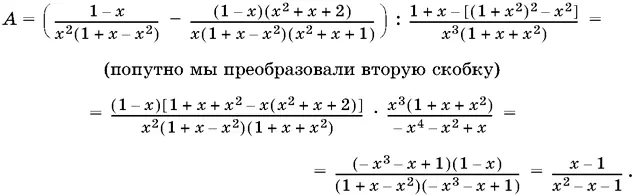
Ответ.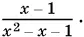

7.3.Приведем первые два слагаемых к общему знаменателю. Получим

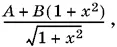
где А и B — соответственно многочлены, входящие множителями в первое и во второе слагаемые.

Раскроем в числителе скобки и приведем подобные. После этого останется

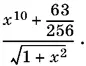
Преобразуем третье слагаемое:

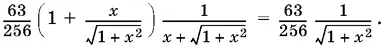
Остается вычесть его из предыдущего результата.

Ответ. 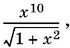это выражение положительно при x ≠ 0.

7.4.Домножив дробь на 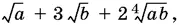получим

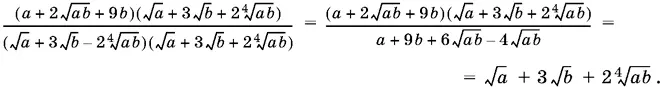
Остается вычесть 2√ b и данное выражение примет вид

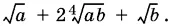
Ответ.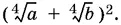

7.5.Вынесем за скобки 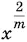и воспользуемся выражением x через а :

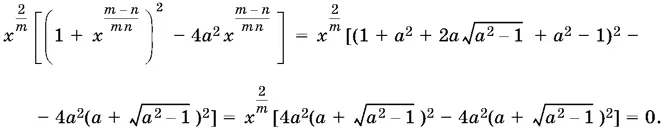
Ответ.0.

7.6.Преобразуем данное выражение:

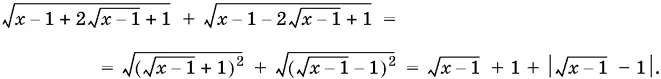
Так как 1 ≤ x ≤ 2, то 0 ≤ x − 1 ≤ 1 и, следовательно, 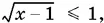т. е. 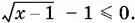Поэтому

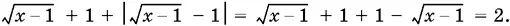
Ответ.2.

7.7.Так как 9 + 4√2 = (2√2 + 1)², то

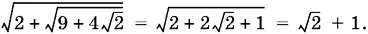
Остается преобразовать

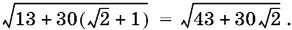
Если догадка, что

43 + 30√2 = 25 + 2 · 5 · 3√2 + 18 = (5 + 3√2)²,

кажется вам неестественной, то воспользуйтесь формулой сложного радикала

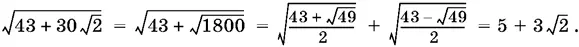
Ответ.5 + 3√2.

7.8.Перепишем данное выражение в виде

( z ² − y ²)( xу + zu ) + ( x ² − u ²)( xу + zu ) + ( y ² − z ²)( xz + уu ) + ( x ² − u ²) × ( xz + уu ) = ( z ² − y ²)( xу + zu − xz − уu ) + ( x ² − u ²)( xу + zu + xz + уu ).

Так как

xу + zu − xz − уu = x ( y − z ) − u ( y − z ) = ( y − z )( x − u ),

xу + zu + xz + уu = ( y + z )( x + u ),

то получим

( z − y )( z + y )( y − z )( x − u ) + ( x − u )( x + u )( y + z )( x + u ) = ( x − u )( y + z )[−( y − z )² + ( x + u )²].

Ответ.( x − u )( y + z )( x + u − y + z )( x + u + y − z ).

7.9.Обозначим

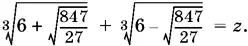
Возведем в куб. Получим

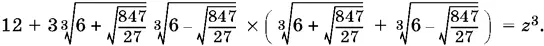
Произведение корней преобразуем так:

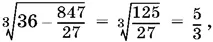
выражение в скобках равно z . Придем к уравнению

z ³ − 5 z − 12 = 0.

Так как z = 3 — корень этого уравнения, в чем убеждаемся проверкой, то преобразуем уравнение к виду

z ³ − 9 z + 4 z − 12 = 0, или ( z − 3)( z ² + 3 z + 4) = 0.

Уравнение z ² + 3 z + 4 = 0 не имеет действительных корней. Следовательно, z = 3, что и требовалось доказать.

7.10.По условию а + b = − с . Возведем в куб

а ³ + b ³ + 3 аb ( а + b ) = − с ³

и заменим а + b на − с . Получим

а ³ + b ³ + с ³ = 3 аbс .

Возведем а + b + с = 0 в квадрат

а ² + b ² + с ² = −2( ab + ас + bc )

и еще раз возведем в квадрат

а 4+ b 4+ с 4+ 2( а ² b ² + а ² с ² + b ² с ²) = 4[ а ² b ² + а ² с ² + b ² с ² + 2( а ² bc + b ² ас + с ² ab )].

Поскольку а ² bc + b ² ас + с ² ab = аbс ( а + b + с ) = 0, то

а 4+ b 4+ с 4= 2( а ² b ² + а ² с ² + b ² с ²).

Преобразуем левую часть тождества, которое нужно доказать:

а 5( b ² + с ²) + b 5( а ² + с ²) + с 5( а ² + b ²) = а ² b ²( а ³ + b ³) + а ² с ²( а ³ + с ³) + b ³ с ²( b ³ + с ³).

Заменим а ³ + b ³ на 3 аbс − с ³ и поступим аналогично с остальными скобками:

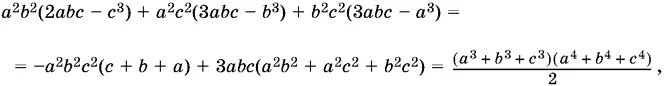
что и требовалось доказать.

7.11.Если данное равенство доказано при x ≥ 0 и любом y , то оно верно для всех x и y . Действительно, пусть x < 0. Тогда левую часть можно записать в виде

|−( x + y )| + |−( x − y )| = |(− x ) − y )| + |(− x ) + y |,

а правую — в виде

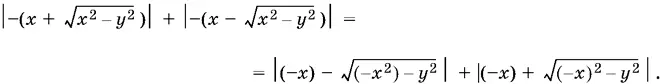
Поскольку − x > 0, то равенство стоящих справа выражений будет доказано.