Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

6.9.Число 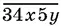должно делиться на 4 и на 9. Это число делится на 4, если две его последние цифры образуют число, делящееся на 4, т. е. либо y = 2, либо y = 6.

Когда y = 2, то x определяется однозначно: так как сумма цифр должна делиться на 9, то x = 4.

Когда y = 6, то в качестве x можно взять либо 0, либо 9.

Итак, получаем три числа.

Ответ.34 452; 34 056; 34 056.

6.10.По условию

1000 а + 100 b + 10 с + 1 = 3(2000 + 100 а + 10 b + с ), где а , b и с — цифры.

После приведения подобных членов получим

700 а + 70 b + 7 с = 5999,

откуда

100 а + 10 b + с = 857.

Это и есть искомое число.

Ответ.857.

6.11.Если p — четное, то p = 2 и p + 2 уже не являются простым. Следовательно, p , p + 2 и p + 4 — три последовательных нечетных числа. Так как p — простое, то либо p = 3, либо p = 3 k + 1, либо p = 3 k + 2 ( k > 0). B первом случае получаем три простых числа 3, 5 и 7. Во втором случае

p + 2 = 3 k + 3 = 3( k + 1),

т. е. p + 2 — число составное. Наконец, в третьем случае

p + 4 = 3 k + 6 = 3( k + 2)

— тоже составное число.

Ответ. p = 3.

6.12.Пусть tg 5° = p / q , где p и q — натуральные. Тогда cos 10° = 1 − tg² 5°/ tg² 5° + 1— тоже рациональное число. Наконец, cos 30° = 4 cos³ 10° − 3 cos 10° также является рациональным числом. Так как cos 30° = √3/ 2, то √3 — рациональное число. Обозначим его через r / s , где r / s — несократимая дробь. Тогда 3 s ² = r ², т. е. r ² делится на 3, а значит, r делится на 3. Пусть r = 3 m ; получим 3 s ² = 9 m ², т. е. s ² = 3 m ², откуда следует, что s делится на 3, а потому дробь r / s сократима. Полученное противоречие доказывает, что tg 5° — число иррациональное.

6.13.Если меньшее из искомых чисел не оканчивается цифрой 9, то по условию суммы цифр двух последовательных натуральных чисел отличаются на 1. Поэтому меньшее число должно оканчиваться одной или несколькими цифрами 9. Если цифра 9 одна, то разность между суммами цифр двух таких последовательных чисел будет равна 8, если цифр 9 две, то эта разность будет равна 17, если три, то 26, если их четыре, то 35, если пять — 44 и т. д. Нас может заинтересовать из этих вариантов только число 44, так как разность двух чисел, каждое из которых делится на 11, тоже должна делиться на 11.

Таким образом, в конце меньшего числа должно быть по крайней мере пять цифр 9. Сумма оставшихся цифр должна быть на 1 меньше числа, которое делится на 11. Например, она может быть равна 10, 21, 32 и т. д. Теперь легко привести примеры:

5 599 999 и 5 600 000, 16 399 999 и 16 400 000,

77 799 999 и 77 800 000, 888 899 999 и 888 900 000.

Этого для решения задачи достаточно. Искать все такие пары не требовалось.

6.14.Сделаем подстановку x = ky и разложим квадратный трехчлен относительно k на множители (при x = 0 и при y = 0 целых решений исходное уравнение не имеет):

3 x ² − 16 xy − 35 y ² = y ²(− k ² − 16 k − 35) = y ²(3 k + 5)( k − 7).

Теперь уравнение можно записать так

y ²(3 k + 5)( k − 7) = −17. (1)

Так как x и y — целые, то k — рациональное число, т. е. k = p / q , где p и q — целые, p ≠ 0, q ≠ 0. После подстановки в (1) получим

( y / q )² (3 p + 5 q )(7 q − p ) = 17. (2)

Каждый из множителей в левой части (2) — целое число. При этом

( y / q )² = 1.

Иначе в правой части было бы два одинаковых целых множителя, отличных от ± 1. Остается рассмотреть варианты:

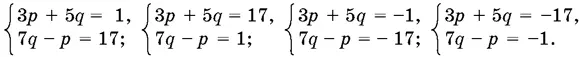
Вторая и четвертая системы не имеют целых решений. А первая и третья дают нам соответственно p 1= −3, q 1= 2; p 2= 3, q 2= −2.

Поскольку ( y / q )² = 1, находим два решения системы.

Ответ.(−3, 2), (3, −2).

6.15.Если x = а , y = b — решение уравнения, то это уравнение имеет еще три решения: (− а , b ), ( а , − b ), (− а , − b ).

Запишем уравнение в виде ( x − 2 y )( x + 2 y ) = 5² · 9 · 89 и рассмотрим только неотрицательные значения сомножителей: x − 2 y ≥ 0, x + 2 y ≥ 0. Кроме того, x + 2 y ≥ x − 2 y . Поэтому нужно рассмотреть только системы:

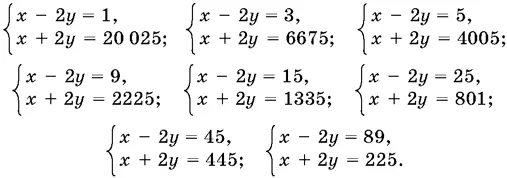
Их решениями будут соответственно:

(10 013, 5006), (3339, 1668), (2005, 1000), (1117, 554), (675, 330), (413, 194), (245, 100), (157, 34).

Каждое из этих восьми решений дает еще 3 решения.

Если решение системы

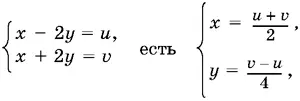
то решение системы

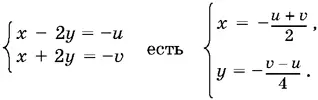
Таким образом, рассмотрение случая, когда число 3² · 5² · 89 разбивается на два отрицательных целочисленных множителя, к новым решениям не приведет.

Ответ.32 целочисленных решения.

6.16.Запишем исходное условие в виде

44 x − 11 = 69( y − x ), или 11(4 x − 1) = 69( y − x ).

Числа 11 и 69 взаимно простые, т. е. не имеют общих натуральных множителей, больших 1. Поэтому число 4 x − 1 кратно 69, а число y − x кратно 11:

4 x − 1 = 69 k , y − x = 11 n ,

где k и n — натуральные числа.

Воспользуемся тем, что 69 k + 1 = 4 x , т. е. левая часть этого равенства делится на 4. Запишем его в виде: 68 k + k + 1 = 4 x , откуда k = 4 m − 1. B качестве k могут быть использованы числа 3, 7, 11, 15, ... Проверим первое из них, которому соответствует минимально возможное значение x : 68 · 3 + 4 = 4 х , т. е. x = 52. Поскольку y = x + 11 n , то рассмотрим значения y по мере возрастания n . Минимальное значение y будет соответствовать минимальному значению n . При n = 1 получим y = 63.

Ответ.(52; 63).

7.1.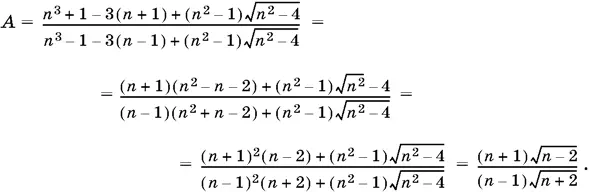

Ответ.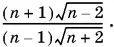

7.2.Перепишем данное выражение так:

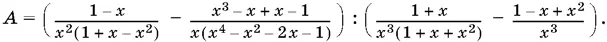
Числитель второй дроби теперь легко разложить на множители. Со знаменателем дело обстоит несколько труднее. Однако в первую очередь нас интересует, делится ли знаменатель на 1 + x − x ². Проверяем с помощью деления углом (проделайте это самостоятельно) и убеждаемся, что