Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

½ KQ · EG + ½( EG + MN ) QR .

Так как KL || AC 1, то LC 1= ¼ A 1 С 1и MN = ½ В 1 D 1= ½ EG . B свою очередь 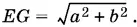Поэтому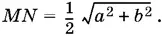

Чтобы вычислить отрезки KQ и QR , спроецируем KR на плоскость основания. Точка Q спроецируется в P , а точка R — в H . Обозначим через S и T проекции точек K и Q на отрезки QP и RH соответственно.

По теореме о трех перпендикулярах АР ⊥ BD . Сравнивая площадь треугольника ADB , получим АР · BD = ab , а так как 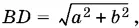то

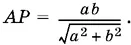
Из подобия треугольников легко получим

AK = ¼ с , RT = ¼ с , QS = ½ с .

Поскольку MN = ½ В 1 D 1, то QR = ½ KQ . Из треугольника KQS находим

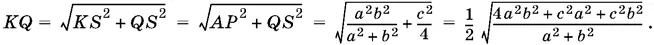
Теперь мы можем вычислить площадь фигуры:

S = ½ KQ · EG + ½ · 3/ 2 EG · ½ KQ = 7/ 8 EG · KQ .

Ответ.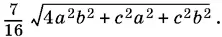

4.10.Чтобы построить тень куба, достаточно построить тень, отбрасываемую верхним основанием. По условию источник света расположен на высоте 2 h . Из подобия треугольников, получающихся при построении тени, следует, что тенью, отбрасываемой верхним основанием куба, будет квадрат A 2 В 2 С 2 D 2(см. рис. P.4.10; также рис. 1.4.10 на с. 132).

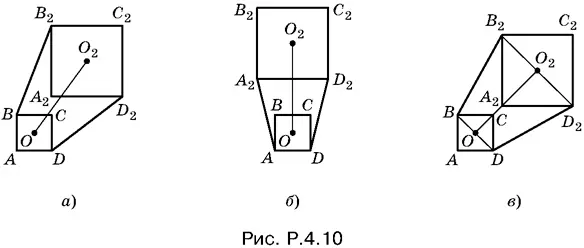
Каждая сторона этого квадрата параллельна соответствующей стороне основания куба и равна 2 h . Отрезок OO 2, соединяющий центры квадратов ABCD и A 2 В 2 С 2 D 2, при вращении источника света не изменяется и равен R . Чтобы получить тень куба, нужно на рис. P.4.10, а построить «внешние» отрезки, соединяющие соответственные вершины квадрата A 1 В 2 С 2 D 2с вершинами нижнего основания куба.

Задача становится плоской. Нужно выяснить, когда площадь полученного многоугольника будет максимальной, если точка О 2вращается вокруг точки О , а стороны квадрата A 2 В 2 С 2 D 2остаются параллельными сторонам квадрата ABCD .

B двух случаях (см. рис. P.4.10, б и в ) площадь будет достигать максимума по сравнению с близкими положениями точки О 2. B самом деле, если точка О 2немного сместится из положения, изображенного на рис. P.4.10, б , вправо или влево по окружности радиуса R , то площадь тени уменьшится, так как уменьшится площадь трапеции АDD 2 A 2: y этой трапеции основания AD и А 2 D 2не изменятся, а высота станет меньше. То же самое произойдет и в случае, изображенном на рис. P.4.10, в . Здесь уменьшится площадь трапеции BDD 2 В 2.

Остается сравнить площади этих двух фигур.

Площадь первой равна

4 h ² + 3 h / 2( R − h / 2),

площадь второй

3√2/ 2 Rh + 5/ 2 h ².

При R > 2 h вторая площадь больше, что и доказывает сформулированное в условии утверждение.

4.11.Острый угол φ между плоскостью основания куба и плоскостью Π не изменится при параллельных переносах куба и при вращении его вокруг оси, перпендикулярной к плоскости Π.

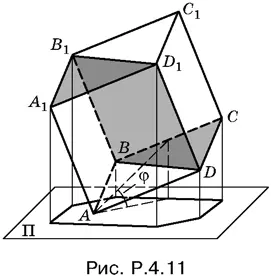
Тень, отбрасываемая кубом, равна тени от заштрихованной на рис. P.4.11 фигуры, которая составлена из двух треугольников A 1 B 1 D 1и BCD и диагонального сечения B 1 D 1 DB . Площадь тени равна

2 · a ²/ 2cos φ + a ²√2 cos ( π/ 2− φ) = a ²(cos φ + √2 sin φ).

Максимум этого выражения равен а ² √3 и достигается при φ = acrtg √2. Таким образом, тень, отбрасываемая кубом, имеет максимальную площадь, равную а ² √3, когда шесть граней куба образуют с плоскостью Π одинаковые углы.

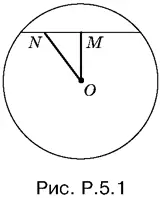
5.1.Из любой точки M (рис. P.5.1) отрезок ON виден под прямым углом. Следовательно, искомое геометрическое место точек — окружность, построенная на отрезке ON , как на диаметре.

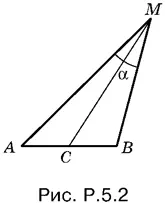
5.2. Пусть точка M принадлежит искомому геометрическому месту точек. По теореме косинусов для треугольника AMB (рис. P.5.2) имеем

AB ² = AM ² + BM ² − 2 AM · BM cos α.

Так как AM · BM cos α = ¾ AB ², то

AM ² + BM ² = 5/ 2 AB ². (1)

Если МС — медиана треугольника АМВ , то

4 MC ² = 2 АМ ² + 2 ВМ ² − АВ ².

Воспользуемся соотношением (1) и заменим 2( АМ ² + ВМ ²) на 5 АВ ²:

4 МС ² = 5 АВ ² − АВ ², т. е. МС = AB .

Итак, искомое геометрическое место точек — окружность радиусом AB с центром в середине AB .

5.3.Докажем вначале, что если точка M лежит на рассматриваемой окружности, то выполняется сформулированное в условии задачи соотношение. Обозначим центр окружности буквой O и выберем на окружности произвольную точку M , отличную от А и С (рис. P.5.3).

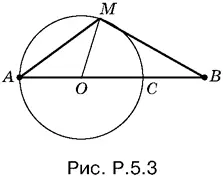
Применим к стороне МВ треугольника АМВ теорему косинусов:

МВ ² = АМ ² + АВ ² − 2 АМ · AB cos А .

Из треугольника АMO находим AM = 2 АO cos А , откуда cos А = AM / 2 AO . По условию АO = AB / 3. Подставляя cos А = 3/ 2 AM / AB в выражение для МВ ², получим МВ ² = АМ ² + АВ ² − З АМ ², т. е. 2 АМ ² + МВ ² = АВ ², что и требовалось проверить.

Простой проверкой легко убедиться, что это соотношение справедливо, если M совпадает с А и если M совпадает с С . B первом случае AM = 0, а МВ = AB и равенство становится очевидным AB ² = АВ ². Во втором случае AM = AC = ⅔ AB , МВ = СВ = ⅓ AB и