Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

Ответ.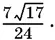

4.3.Пусть K — точка пересечения AO 1и C 1 C (рис. P.4.3). Соединим K с центром Q боковой грани BB 1 C 1 C и получим сечение куба. Так как Q — центр симметрии квадрата B 1 C 1 CB , то B 1 E = FC . Проведем O 1 C 1и AC . Отрезок O 1 C 1— средняя линия в треугольнике AKC , и, следовательно, KC 1= C 1 C .

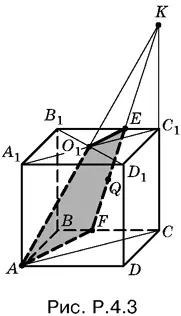
Треугольники KFC и KEC 1подобны с коэффициентом подобия 2. Поэтому FC = 2 EC 1. Так как FC = В 1 Е , то отношение отрезков B 1 E к ЕС 1равно 2.

Ответ.2.

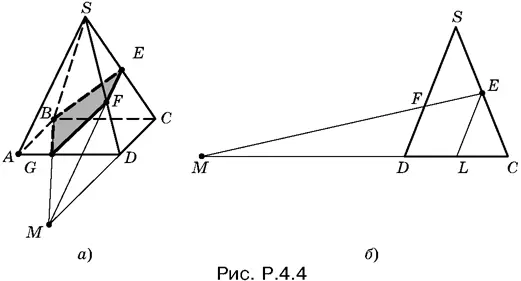
4.4.Пусть высота данной пирамиды h , сторона основания а . Найдем объем фигуры, лежащей под сечением BEFG (рис. P.4.4, а ), как разность объемов пирамид EBCM и FGDM .

Объем первой пирамиды равен

⅓ h / 2 3 a ²/ 2= ¾(⅓ ha ²) = ¾ v ,

где v — объем данной пирамиды.

Чтобы найти высоту пирамиды FGDM , сделаем чертеж плоскости, в которой лежит грань SDC (рис. P.4.4, б ). Проведем EL параллельно SD . Так как E — середина SC , то DL = ½ DC = a / 2. Из подобия треугольников MEL и MFD найдем

FD / EL = MD / ML = 2 a / 2,5 a = 4/ 5.

Нетрудно проверить (сделайте это самостоятельно), что высота пирамиды FGDM равна 4/ 5высоты EBCM , т. е. 4 h / 10.

Из подобия треугольников MGD и MBC (см. рис. P.4.4, а ) найдем GD = 2 a / 3. Это означает, что объем пирамиды FGDM равен

⅓ 4 h / 10 2 a ²/ 3= 4/ 15(⅓ ha ²) = 4/ 15 v ,

Таким образом, объем фигуры, лежащей под сечением, равен

¾ v − 4/ 15 v = 29/ 60 v .

Ответ. 29/ 31.

4.5.Сечение AMND и диагональная плоскость ASC разбивают данную пирамиду на четыре части. Так как высота пирамиды NACD (рис. P.4.5) вдвое меньше высоты данной пирамиды, а площадь основания вдвое меньше площади основания ABCD , то ее объем равен v / 4, где v — объем данной пирамиды.

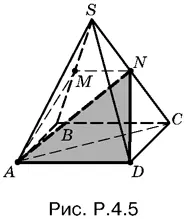
Рассмотрим пирамиды ASBC и ASMN с общей вершиной A . Их высоты равны, а площадь основания первой в четыре раза больше. Следовательно, их объемы относятся, как 4 : 1. Таким образом, на долю пирамиды ABMNC приходится 3 v / 8.

Теперь можно найти, какую часть объема пирамиды составляет фигура, расположенная под сечением:

¼ v + 3/ 8 v = 5/ 8 v .

Ответ. 5 : 3.

4.6.Соединим точки P , Q и R с вершиной A (рис. Р.4.6), после чего соединим их между собой.

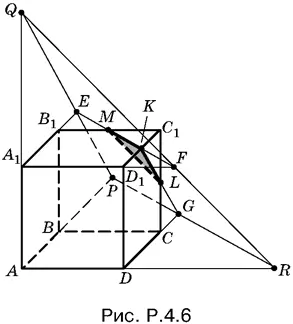
Продолжим A 1 B 1до пересечения с QP в точке E и A 1 D 1до пересечения с QR в точке F . Обе точки E и F лежат в плоскости верхнего основания, а EF — след сечения в этой плоскости, который пересекает верхнюю грань куба по отрезку MK .

Продолжим DC до пересечения с PR в точке G и соединим K с G . На ребре СС 1получим точку L , принадлежащую сечению.

Из подобия треугольников QА 1 Е и QAP следует, что А 1 Е = А 1 Q = 3 a / 2, где а — ребро куба.

Следовательно, В 1 Е = а / 2. Аналогично D 1 F = а / 2и СG = а / 2, откуда следует, что МС 1= KC 1= LC 1= а / 2. Объем пирамиды MC 1 LK равен а ³ : 48.

Ответ.1 : 47.

4.7.Пусть MN = а (рис. P.4.7).

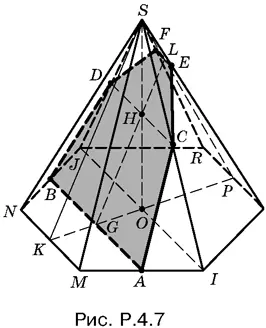
Тогда aSK = 2 Q . Выразим искомую площадь через а и SK . Отрезок AB — средняя линия трапеции IМNJ , а отрезок DC — средняя линия треугольника SIJ . Поэтому

AB = 3/ 2 а , DC = а .

Из подобия треугольников SOK и HOG следует, что HG = ½ SK . Осталось определить HL и EF :

HL = GL − GH = ¾ SK − ½ SK = ¼ SK ;

из подобных треугольников FSL и RSP

EF / a = SL / SP = KG / KP = ¼, т. е. EF = а / 4.

Теперь можно подсчитать площадь сечения, которая равна

½( AB + CD ) GH + ½( CD + FE ) HL = ½( 5 a / 4 GH + 5/ 4 aHL ) = 5 a / 4(½ SK + 1/ 8 SK ) = 25 a / 32 SK .

Так как aSK = 2 Q , то площадь сечения можно выразить через Q .

Ответ. 25/ 16 Q .

4.8.Спроецируем С 1 С на плоскость основания призмы (рис. P.4.8). Отрезок EK — средняя линия в треугольнике С 1 CF .

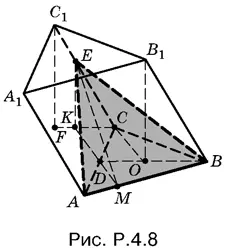
Через точки K и D проведем прямую, которая пересечет AB в точке M . Докажем, что ЕМ — высота в треугольнике АВЕ .

Поскольку KC = ½ FC , а DO = ½ OB ( ABC — правильный треугольник) и FC = OB (треугольники C 1 FC и В 1 ОВ равны), то KC = DO. Покажем, что KC || DO. B самом деле, так как OB ⊥ AC , то и ВВ 1 ⊥ AC . Следовательно, CC 1 ⊥ AC , а значит, и KC ⊥ AC . Итак, KC и DO параллельны, а фигура KCOD — параллелограмм. Теперь мы можем воспользоваться тем, что отрезок KM параллелен CO , а потому перпендикулярен к AB . Отсюда следует, что ЕМ — высота в треугольнике АВЕ .

Остаются простые вычисления:

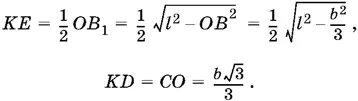
Площадь треугольника ADB можно найти двумя способами: ½ DM · AB = ½ DВ · AD , т. е. bDM = b ²√3/ 4, откуда MD = b √3/ 4. Теперь найдем ЕМ :

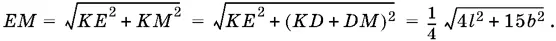
Ответ.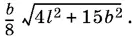

4.9.B диагональной плоскости ВВ 1 D 1 D (рис. P.4.9) проведем через точку F отрезок EG , параллельный ВD .

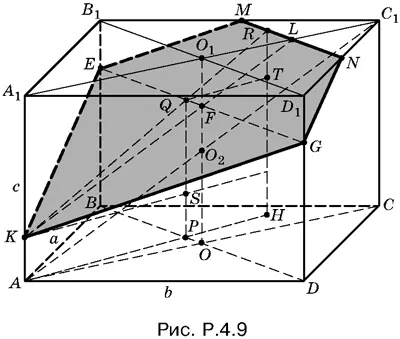
B другой диагональной плоскости AA 1 С 1 С проведем через точку F отрезок KL || АС 1. B плоскости верхнего основания построим отрезок MN || В 1 D 1и проходящий через точку L . Точки K , G , N , M , E являются вершинами сечения, площадь которого мы должны вычислить. Это сечение — пятиугольник, разбивающийся на треугольник EKG и трапецию EGNM . Если KR — высота треугольника, а Q — точка пересечения KR и EG , то площадь пятиугольника равна