Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

Проведем теперь все вычисления.

Из треугольника О 3 АО 2находим

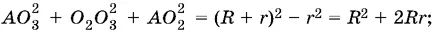
из треугольника О 3 АВ находим

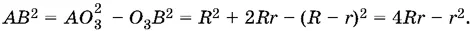
Следовательно,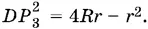

Вычисляем

P 3 Р ² = CO ² = ( R + x )² − ( R − x )² = 4 Rx

и

Р 1 Р ² = ЕО ² = O 1 O ² − O 1 Е ² = ( r + x )² − ( r − x )² = 4 rx .

B треугольнике P 1 DР известна гипотенуза Р 1 Р . Катет Р 1 D = r , а катет

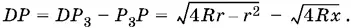
По теореме Пифагора Р 1 Р ² = Р 1 D ² + DP ², т. е.

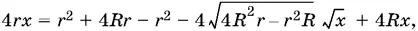
или

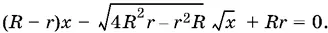
Решая это уравнение, находим

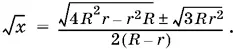
Хотя правая часть в обоих случаях положительна, нужно взять только знак минус, так как второе значение для √ x оказывается больше √ r , что невозможно.

Ответ.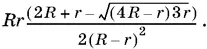

3.46.Пусть O 1и O 2— центры двух равных шаров с радиусом R , а O 3— центр третьего шара радиусом r (рис. P.3.46). Треугольник O 1 O 3 F прямоугольный, т. е.

O 1 O 3² = O 1 F ² + O 3 F ².

Так как O 1 O 3= R + r , O 1 F = R − r , то остается вычислить O 3 F . Из треугольника BDE , в котором DB = O 3 F , имеем

DB ² = DE ² + ЕВ ².

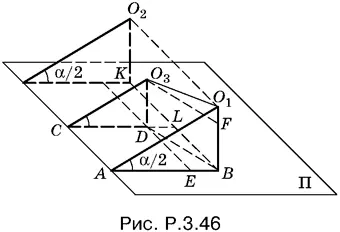
Длину отрезка EB можно найти как AB − AE . Но AB = R ctg α/ 2(из треугольника O 1 AB ), а AE = CD = r ctg α/ 2(из треугольника O 2 CD ). Таким образом,

EB ² = ( R ctg α/ 2− r ctg α/ 2)².

Отрезок DE можно определить, если воспользоваться условием, что шары O 1и O 2касаются. Отрезок O 1 O 2равен 2 R и параллелен плоскости Π. Следовательно, KB = 2 R и DE = LB = R .

Величина DB ² теперь найдена:

DB ² = R ² + ctg² α/ 2( R − r )²,

и теорема Пифагора для треугольника O 1 O 3 F примет вид

( R + r )² = ( R − r )² + R ² + ctg² α/ 2( R − r )².

Раскрыв скобки в членах, не содержащих множителя ctg² α/ 2, найдем

ctg² α/ 2= 4 Rr − R ²/ ( R − r )².

По условию r / R = m ; разделим числитель и знаменатель правой части почленно на R ²

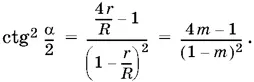
Число m всегда меньше единицы, так как по условию r меньше R . Кроме того, 4 m − 1 ≥ 0, так как слева стоит квадрат. Но ctg α/ 2= 0, если α/ 2= π/ 5и α = π, что невозможно. Поэтому 4 m − 1 > 0 и m > ¼.

Ответ.При ¼ < m < 1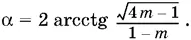

3.47.Обозначим центры шаров буквами O 1, O 2и O 3, а их проекции на плоскость P через A , B и C . Треугольник ABC (рис. P.3.47) равносторонний со стороной 2 R , а точка O — проекция вершины S конуса — будет центром этого треугольника.

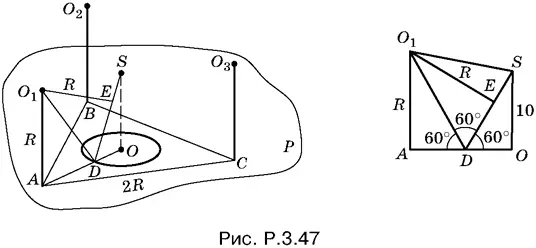
Образующую конуса, которой касается шар с центром в точке O 1, обозначим через SD , а точку касания — буквой E . Отрезок O 1 E перпендикулярен SD и равен R . Так как данный конус равносторонний, то угол между образующей и ее проекцией на основание конуса равен 60°. По условию SO = 10, следовательно, DO = 10 · ctg 60° = 10/ √3. Отрезок AO находим из треугольника ABC :

AO = 2 R / √3.

Таким образом, AD = 2 R − 10/ √3. Угол ADE равен 120°, а луч O 1 D делит его пополам. Из прямоугольного треугольника AO 1 D

R = AD tg 60°, т.е. R = 2 R − 10/ √3√3.

откуда находим R .

Ответ.10 см.

3.48.Пусть SO 1и SO 2— оси соседних конусов (рис. P.3.48). Тогда середина C отрезка O 1 O 2лежит на общей образующей этих конусов.

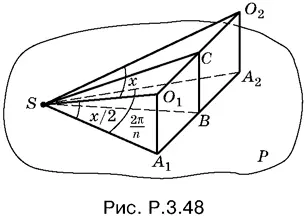
Угол O 1 SO 2равен углу в осевом сечении конуса, обозначим его через x . Тогда углы O 1 SA 1и О 2 SA 2равны x / 2. Проекции осей SO 1и SO 2на плоскость P лежат на образующих, по которым происходит касание конусов с плоскостью P . Так как конусов n , то угол A 1 SA 2= 2π/ n .

Отрезок SO 1можно выразить через А 1 В двумя способами:

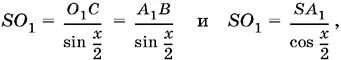
а так как 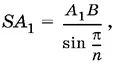то

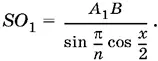
Приравнивая полученные для SO 1выражения, получим tg x / 2= sin π/ n .

Ответ.x = 2 acrtg [sin π/ n ].

3.49.Так как угол AOB (рис. P.3.49, а , б ) прямой, то точки А и О лежат на сфере, построенной на AB , как на диаметре. Следовательно, все внутренние точки отрезка АО лежат внутри этой сферы. Поскольку центр сферы, радиус которой мы ищем, лежит на АО , то возможно лишь внутреннее касание сфер.

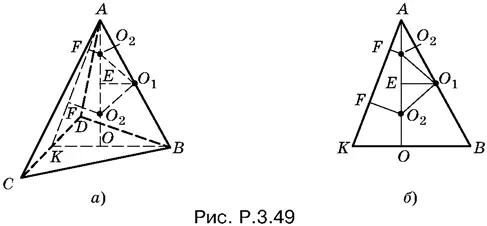
Центр О 2вписанной сферы соединим с точкой F , в которой происходит касание сферы с одной из граней. Из подобия треугольников FО 2 A и OKA имеем

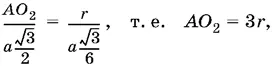
где r — искомый радиус.