Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

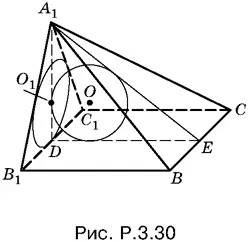
Рассмотрим треугольник DA 1 E . Он прямоугольный и его площадь, с одной стороны, равна ½ A 1 D · DE , а с другой стороны, R / 2( A 1 D + DE + A 1 E ). Поскольку

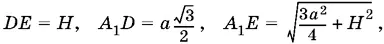
получаем уравнение относительно H , которое после подстановки а = 2√3 R и возведения в квадрат принимает вид H ² = 4 HR , откуда H = 4 R .

Ответ.12√3 R ³.

3.31.Центр шара, касающегося трех ребер правильного тетраэдра, исходящих из общей вершины, должен лежать на биссектрисе соответствующего трехгранного угла, которая совпадает с высотой тетраэдра, опущенной из этой же вершины. Поскольку все четыре биссектрисы пересекаются в одной точке — центре вписанного в тетраэдр шара, достаточно рассмотреть треугольник SOA (рис. P.3.31), где SO — высота тетраэдра, SA — его ребро, а O 1— центр искомого шара и шара, вписанного в тетраэдр.

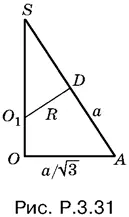
Треугольники SAO и SO 1 D подобны. B первом известны все стороны, во втором SO 1= a √6/ 4. = . Это позволяет вычислить R .

Ответ. a √2/ 4.

3.32.Если один куб расположен внутри другого, а вершина O y них общая, то диагонали этих кубов, проходящие через O , лежат на одной прямой. Поэтому из всех подобных кубов, которые можно поместить в параллелепипед, мы выберем максимальный.

Пусть с < а и с < b . Тогда в параллелепипед можно поместить куб с ребром с (рис. P.3.32).

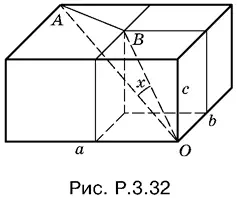
Вычислим все стороны треугольника ABO и воспользуемся теоремой косинусов:

AB ² = AO ² + BO ² − 2 AO · BO cos x ,

AO ² = а ² + b ² + с ², BO ² = 3 c ²,

AB ² = ( а − с )² + ( b − с )².

Для определения cos x получим уравнение

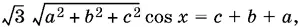
которое симметрично относительно а , b и с , а потому не зависит от соотношения между этими величинами. Убедитесь сами в том, что cos x не будет больше единицы при любых а , b и с .

Ответ.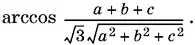

3.33.Разность углов А и С равна φ, BD — биссектриса угла B в треугольнике ABC (рис. P.3.33).

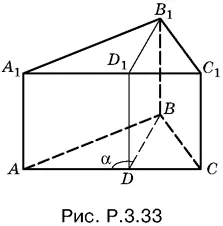
Вычислим угол а:

α = B / 2+ С = π − A − C / 2+ С = π/ 2+ C − A / 2= π/ 2+ φ/ 2.

Объем призмы равен произведению АА 1на площадь основания ABC , т. е.

АА 1 (½ AD · DB sin α + ½ DC · DB sin α) = ½ АА 1· DB · AC sin α = ½ aS cos φ/ 2.

Ответ.½ aS cos φ/ 2.

3.34.Пусть выбраны диагонали С 1 D и В 1 С (рис. P.3.34). Так как В 1 С || А 1 D и С 1 D || В 1 A , то плоскости А 1 С 1 D и АВ 1 С параллельны. Расстояние между В 1 С и С 1 D равно расстоянию между этими плоскостями.

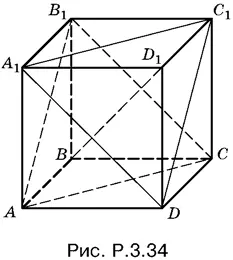
Обе плоскости А 1 С 1 D и АВ 1 С перпендикулярны к диагонали BD 1. Поэтому искомое расстояние равно разности между отрезком BD 1и удвоенной высотой пирамиды D 1 А 1 С 1 D . Объем этой пирамиды равен a ³/ 6, а площадь основания А 1 С 1 D равна а √3/ 2, следовательно, высота h = a / √3. Так как BD 1= a √3, то искомое расстояние равно a √3 − 2 a / √3= a / √3.

Ответ. a / √3.

3.35.Из соображений симметрии ясно, что точка O лежит на диагонали AC 1куба. Для доказательства достаточно установить, что плоскость KMN (рис. P.3.35) перпендикулярна к АС 1и что АС 1проходит через точку O 1, являющуюся центром треугольника KMN .

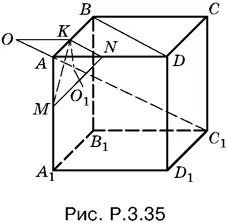
По теореме о трех перпендикулярах АС 1 ⊥ BD . Следовательно, АС 1 ⊥ KN . Аналогично прямая АС 1перпендикулярна к KM или MN , т. е. АС 1— перпендикуляр к плоскости KMN .

Треугольник KMN равносторонний. Так как AK = AN = AM , то из равенства соответствующих треугольников, имеющих общие вершины в точках А и О 1, получаем KO 1= NO 1= MO 1.

Мы доказали, что центр О сферы лежит на продолжении отрезка АС 1.

Так как AK — биссектриса в треугольнике OKO 1, то 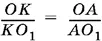. Отсюда найдем OK = R , выразив остальные отрезки через ребро куба:

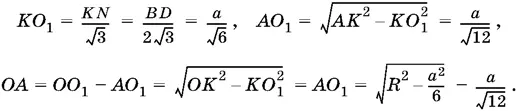
Подставив все эти выражения в пропорцию 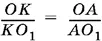, получим уравнение относительно R . После простых преобразований это уравнение запишется в виде

6 R ² − 2√6 aR − 3 а ² = 0.

Геометрический смысл имеет только положительный корень.

Ответ.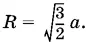

3.36.Докажем вначале, что каждая сторона четырехугольника параллельна биссектральной плоскости двугранного угла, образованного данными взаимно перпендикулярными плоскостями. Перенесем сторону четырехугольника параллельно себе так, чтобы одна из ее вершин лежала на ребре этого двугранного угла (рис. P.3.36, а ). Полученный отрезок RS спроецируем на плоскости P и Q . Так как проекции при параллельном переносе не изменяются, то RS 1= RS 2= 1. Построим линейный угол S 1 TS 1, измеряющий двугранный угол между плоскостями P и Q , и соединим точки S и T . Треугольники RS 1 T и RS 2 T и треугольники RS 1 S и RS 2 S попарно равны, т. е. прямоугольные треугольники S 1 ST и S 2 ST — равные и равнобедренные. Следовательно, углы STS 1и STS 2равны 45°, а это означает, что сторона данного четырехугольника параллельна биссектральной плоскости. Проведя аналогичные рассуждения для каждой стороны, придем к выводу, что плоскость четырехугольника параллельна биссектральной плоскости.