Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

Ответ. b / c .

3.19.Объем пирамиды SABC (рис. P.3.19) равен удвоенному объему пирамиды с основанием DSC и высотой AD .

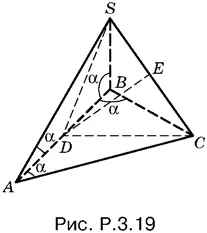
Так как AD = a / 2, то этот объем равен Sa / 6, а объем всей пирамиды равен Sa / 3, где через S обозначена площадь SDC .

Проведем высоту DE и вычислим EC и DE.

Треугольник CAS равнобедренный ( AS = AC ), поэтому

EC = AC sin α/ 2= a / 2 cos αsin α/ 2.

Так как DC = a / 2tg α, то

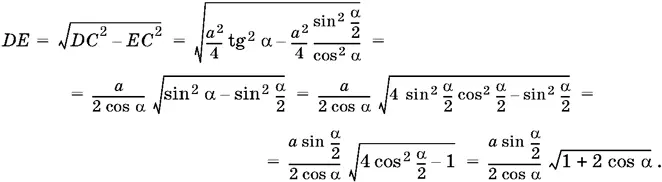
Остается вычислить объем:

V = aS / 3= a / 3· DE · EC .

Ответ.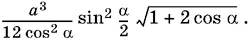

3.20.Рассмотрим два случая:

α ≤ π/ 2, α > π/ 2.

Если угол α не тупой, то (рис. P.3.20, a ) CD = SD = AB / 2.

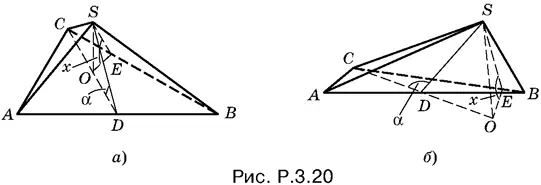
Пусть SO — высота пирамиды, SD и SE — высоты в треугольниках ASB и CSB . Из треугольника SOD

OS = SD sin α = A B / 2sin α, OD = A B / 2cos α.

B треугольнике COE угол OEC прямой, а угол OCE равен 45°. Поэтому

OE = OC / √2= 1/ √2( CD − OD ) = AB / 2√2(1 − cos α).

Теперь можно найти тангенс искомого угла:

tg x = OS / OE = √2 ctg α/ 2.

Если угол α тупой, то (рис. P.3.20, б ) снова получим CD = SD = AB / 2. Высота OS равна

OS = SD sin (π − α) = AB / 2sin α,

отрезок OD равен

OD = SD cos (π − α) = − AB / 2cos α

(угол α тупой и cos α < 0). Треугольник СОЕ тоже прямоугольный и равнобедренный. Поэтому

OE = CO / √2= 1/ √2( CD + OD ) = AB / 2√2(1 − cos α).

Так как для OE и OS получились такие же значения, как в первом случае, то и окончательный результат не изменится.

Ответ. x = arctg (√2 ctg α/ 2).

3.21.Проведем в треугольнике ABC (рис. P.3.21) высоту BD и соединим точку D с вершиной S пирамиды. Так как ребро SB образует равные углы с ребрами SC и SA , то SD — биссектриса угла ASC .

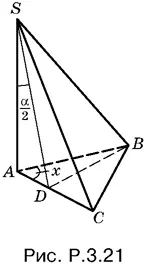
Рассмотрим прямоугольный треугольник ABD . B нем

AD = SA · tg α/ 4, AB = SA · tg α, т. е.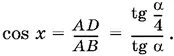

Так как α — угол прямоугольного треугольника, то 0 < α < π/ 2, а потому tg α/ 4< tg α и правая часть уравнения меньше единицы.

Ответ.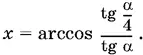

3.22.Пусть M — середина AB. Тогда медианы СМ и DM (рис. P.3.22) являются одновременно высотами в равнобедренных треугольниках ABC и ABD . Следовательно, прямая AB перпендикулярна к плоскости CMD , а потому и к прямой CD , лежащей в этой плоскости. Треугольник CMD равнобедренный, так как СМ и MD — медианы, проведенные к общей стороне в равных треугольниках. Следовательно, его высота MK будет одновременно и медианой. Итак, отрезок KM , соединяющий середины AB и CD, есть общий перпендикуляр к этим ребрам. Поэтому центр описанного около тетраэдра ABCD шара должен лежать на этом отрезке.

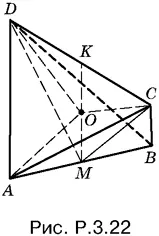
Из треугольников MDB и MDK последовательно находим MD = √65, MK = 7. С другой стороны, из треугольников OKD и AMO находим 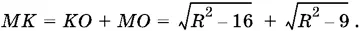Получаем уравнение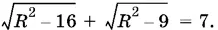

Ответ. R = 5.

3.23.Проведем через точку O (рис. P.3.23) сечение B 1 EC 1пирамиды, перпендикулярное к стороне SA . Тогда угол B 1 EC 1равен α, а OE = а. Так как пирамида правильная, то в силу симметрии треугольник B 1 EC 1равнобедренный, а B 1 C 1и BC параллельны.

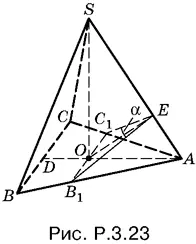
Чтобы связать высоту SO с элементами треугольника B 1 EC 1, рассмотрим треугольник SOA , для которого воспользуемся сравнением площадей:

SO · OA = OE · SA . (4)

Выразим все участвующие в этом соотношении отрезки через а , α и h :

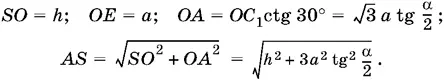
Подставив в уравнение (4) и возведя затем обе части уравнения в квадрат, получим уравнение

3 h ² tg² α/ 2− h ² = 3 a ² tg² α/ 2,

откуда

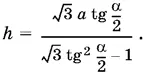
Чтобы привести это выражение к виду, удобному для логарифмирования, преобразуем выражение, стоящее в знаменателе под радикалом:

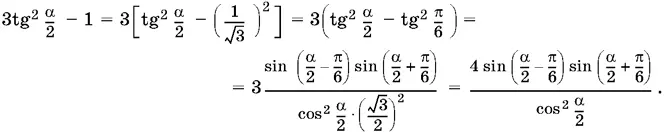
Ответ.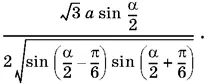

3.24.Если в сечении образуется квадрат, то плоскость сечения пересекает все четыре грани пирамиды. Кроме того, отрезок KL параллелен MN , т. е. параллелен плоскости основания, а следовательно, и ребру AB .

Аналогично отрезки KM и LN параллельны ребру DC . Итак, если в сечении пирамиды — квадрат, то плоскость сечения должна быть параллельной двум скрещивающимся прямым, на которых лежат ребра AB и DC .

Докажем обратное: если провести сечение пирамиды, плоскость которого параллельна AB и DC , то в сечении получится прямоугольник. B самом деле, то, что это будет параллелограмм, устанавливается непосредственно. Спроецировав DC на плоскость основания (рис. P.3.24), мы убедимся в том, что MN и EC взаимно перпендикулярны. Отсюда следует, что прямым будет угол между DC и MN , а значит, и между LN и MN . Таким образом, KLMN — прямоугольник.

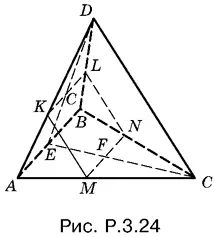
Мы доказали, что в сечении можно получить прямоугольник только с помощью плоскости, параллельной двум скрещивающимся ребрам.