Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

Ответ. 1/ 27.

3.13.Пусть О 1, О 2и О 3— точки пересечения медиан соответствующих граней (на рис. P.3.13 изображены лишь О 1и О 2), О — центр шара.

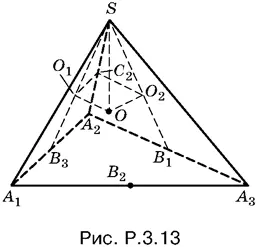
Прямоугольные треугольники SO 1 О , SO 2 О и SO 3 О равны ( О 1 О = О 2 О = О 3 О , OS — общая гипотенуза). Следовательно, SO 1= SO 2= SO 3, и поэтому SB 1= SB 2= SB 3.

Докажем теперь, что треугольник А 1 А 2 А 3правильный. Для этого достаточно установить равенство треугольников A 2 SB 1и A 2 SB 3, т. е. любых соседних из шести таких треугольников. Установим в них равенство углов при вершине S . Пусть C 2— точка пересечения плоскости О 1 ОО 2с ребром SA 2. Прямоугольные треугольники О 1 SC 2и О 2 SC 2тоже равны. Отсюда углы О 1 SC 2и О 2 SC 2равны и, следовательно, равны треугольники B 1 SA 2и B 3 SA 2. Таким образом, В 1 А 2= В 3 А 2, т. е. А 2 А 3= А 1 А 2. Итак, в основании пирамиды лежит правильный треугольник.

Из равенства треугольников B 1 SA 2и B 3 SA 2следует также равенство треугольников A 1 SA 2и A 2 SA 3, т. е. равенство всех боковых ребер. Это означает, что вершина S проецируется в центр основания А 1 А 2 А 3. Тем самым доказано, что пирамида правильная.

3.14.Достроим пирамиду до полной. Все параллельные сечения пирамиды подобны. Составим схематический рис. P.3.14, на котором А и B — стороны квадратов, равновеликих основаниям, M — сторона квадрата, равновеликого сечению, проходящему через середину высоты данной усеченной пирамиды. Последнее условие мы запишем так:

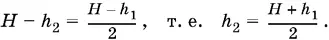
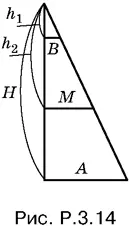
Из подобия треугольников, изображенных на рис. P.3.14, следует, что

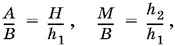
откуда

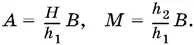
Составим среднее арифметическое величин А и B :

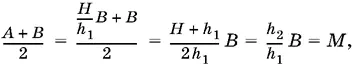
что и требовалось доказать.

3.15.Достроим треугольник ABC до параллелограмма ABCE (рис. P.3.15). Угол DAE равен углу между AD и BC . Обозначим его через x .

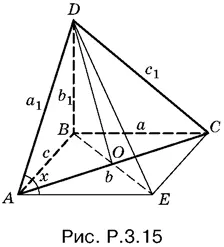
B треугольнике DAE

AD = а 1, AE = а .

Вычислим DE . Так как в дальнейшем мы воспользуемся теоремой косинусов, то удобнее находить DE ².

Отрезок DO является медианой в треугольниках ADC и BDE :

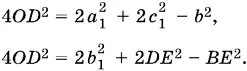
Чтобы найти DE ², достаточно вычислить BE ². Но ВЕ — диагональ параллелограмма ABCЕ , т. е. ВЕ ² = 2 а ² + 2 с ² − b ². Следовательно,

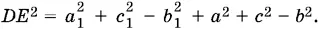
Применим к треугольнику ADE теорему косинусов:

DE ² = a 1² + a ² − 2 aa 1cos x .

Приравнивая два выражения для DЕ ², найдем cos x . При этом следует иметь в виду, что по определению угла между скрещивающимися прямыми x — острый угол.

Ответ.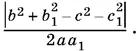

3.16.Плоскость ABE (рис. P.3.16) делит тетраэдр на две пирамиды SABE и CABE с общим основанием ABE .

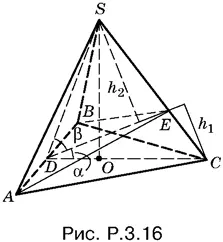
Так как отношение объемов дано, а основание у пирамиды общее, то h 2: h 1 = 5 : 3, в силу же равенства SD = CD имеем

sin α/ sin β= 3/ 5, т.е. sin α = 3/ 5sin β.

Кроме того, так как тетраэдр правильный, углы α и β образуют угол SDO , косинус которого равен 1. Поэтому

cos α cos β − sin α sin β = ⅓.

Выразив в этом уравнении sin β и cos β через sin α (так как пирамида правильная, углы α и β острые), получим

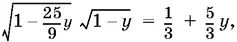
где y = sin² α.

Возведем в квадрат и раскроем скобки; найдем y = 2/ 11 и вычислим tg α:

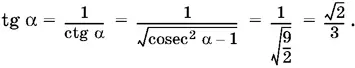
Поскольку sin² β = 25/ 9sin² α = 50/ 99, то аналогично найдем tg β.

Ответ. 5√2/ 7, √2/ 3.

3.17.Треугольники DAM и DMS (рис. P.3.17) имеют общую высоту, проведенную из вершины D . Поэтому отношение их площадей равно отношению оснований AM и MS .

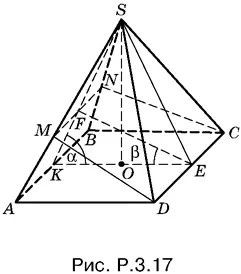
Из подобия треугольников MSF и ASK следует, что AM : MS = KF : FS .

Отрезки KF и FS выразим через KE . По теореме синусов для треугольника KFE имеем

KF = KE sin β/ sin (α + β).

Так как KS = KE / 2 cos α, то

FS = KS − KF = KE / 2 cos α− KE sin β/ sin (α + β)= KE sin (α − β)/ 2 cos α sin (α + β)

(впрочем, это можно установить и непосредственно из треугольника EFS ).

Остается найти отношение KF : FS .

Ответ. 2 sin β cos α/ sin (α − β).

3.18.По условию высоты DO пирамиды проходит через точку пересечения высот основания. Поэтому, соединив точку О с вершиной С и продолжив до пересечения с AB , получим отрезок СЕ , являющийся высотой треугольника ABC , опущенной на сторону AB (рис. P.3.18).

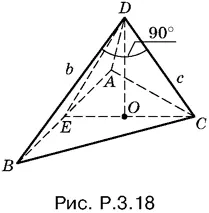
Прямая AB перпендикулярна к DO и EC , следовательно, прямые AB и CD тоже перпендикулярны друг другу. Таким образом, прямая CD перпендикулярна к двум прямым BD и AB плоскости ABD , а потому перпендикулярна к прямой AD . Мы доказали, что угол ADC прямой. Аналогично доказывается, что прямые BD и AD тоже перпендикулярны.

Теперь нетрудно ответить на вопрос задачи: площадь треугольника ADB равна ½ b · AD , а площадь треугольника ADC равна ½ с · AD . Отношение площадей равно отношению неравных катетов.