Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

Этот прямоугольник будет квадратом, если MN = MK . Из подобия треугольников ADC и AMK находим MK / CD = AM / AC , причем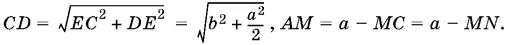

Подставляя в первоначальное отношение, получим

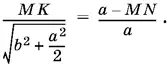
Так как MK = MN , то получим уравнение относительно стороны квадрата, из которого

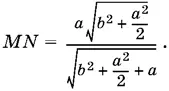
Ответ.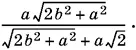

3.25.Расположим пирамиду так, как показано на рис. P.3.25.

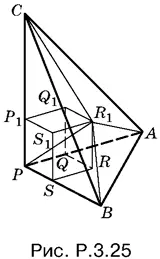
Соединим вершину R 1куба с вершинами пирамиды. Пирамида АBCР разобьется на три пирамиды: R 1 ABP , R 1 ACP , R 1 BCP , y которых общая вершина R 1и одинаковая высота x , равная по длине ребру куба. Из сравнения объемов получим

1/ 6 abc = 1/ 6( xab + xbc + xac ),

откуда найдем x .

Ответ. abc / ab + bc + ac .

3.26.Верхнее основание куба будет вписано в равносторонний треугольник A 1 B 1 C 1(рис. P.3.26) подобный основанию ABC пирамиды.

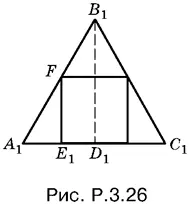
Выразим сторону A 1 C 1треугольника A 1 B 1 C 1через сторону вписанного квадрата:

A 1 C 1= 2 A 1 E 1+ a = 2 a ctg 60° + a = a (1 + 2/ √3).

Площадь треугольника A 1 B 1 C 1тогда равна 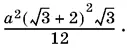Так как треугольники ABC и A 1 B 1 C 1подобны и расстояние первого от центра подобия равно h , а расстояние второго равно h − а , то отношение площадей равно h ²/ ( h − a )². Поэтому площадь треугольника ABC равна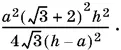

Ответ.

3.27.Пусть трехгранный угол пересечен некоторой плоскостью и в сечении образовался треугольник со сторонами a, b и с (рис. P.3.27).

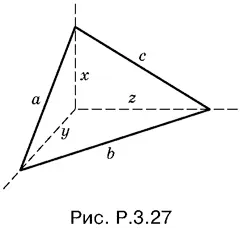
Обозначим через x , y и z боковые ребра образовавшейся пирамиды, если ее вершиной считать вершину данного трехгранного угла. Тогда объем этой пирамиды равен xyz / 6. Поскольку все плоские углы, образующие трехгранный угол, прямые, имеем

x ² + y ² = a ², y ² + z ² = b ², z ² + x ² = с ².

Сложим эти уравнения, найдем x ² + y ² + z ² = ½( а ² + b ² + с ²). Теперь легко определить x , y и z . Таким образом,

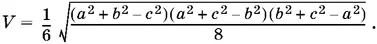
Если треугольник в сечении тупоугольный и а ≤ b < с , то а ² + b ² < с ², т. е. первая скобка под корнем отрицательна, в то время как остальные положительны. Если же треугольник в сечении прямоугольный, то одна из скобок обращается в нуль. Таким образом, нет сечения трехгранного угла, которое не было бы остроугольным треугольником.

3.28.Осуществив построения, изображенные на рис. P.3.28, постараемся вычислить объем данной пирамиды как удвоенный объем пирамиды AODC с вершиной в точке A (равенство объемов AODC и BODC станет очевидным из дальнейшего). Докажем вначале, что AFBE — прямоугольник. Из равенства треугольников CFB и DEA следует, что EA = BF . Аналогично BE = FA . Следовательно, AFBE — параллелограмм. Но EF = AB , а потому эта фигура — прямоугольник. Чтобы найти площадь треугольника DOC , нужно вычислить его высоту CF , для чего достаточно знать стороны прямоугольника AFBE .

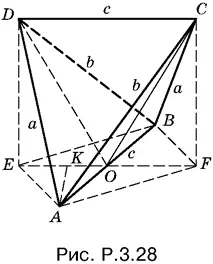
Отрезок CF может быть найден из двух прилегающих к нему прямо угольных треугольников. С одной стороны, CF ² = BC ² − BF ², с другой стороны, CF ² = AC ² − AF ², т. е. BF ² − AF ² = а ²− b ².

Составим систему уравнений:

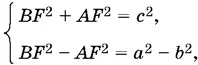
из которой найдем BF ² = ½( а ² − b ² + с ²), AF ² = ½( с ² − а ² + b ²). Теперь можно вычислить CF и AK :

CF ² = а ² − ½( а ² − b ² + с ²) = ½( а ² + b ² + с ²),

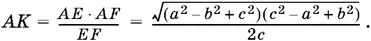
Объем пирамиды ABCD равен 2 · ⅓ AK (½ DC · CF ).

Ответ.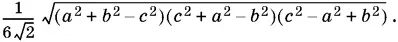

3.29.Расположим пирамиду ABCD так, как показано на рис. P.3.29, а . Воспользуемся методом сравнения объемов по отношению к телу ANBMCD .

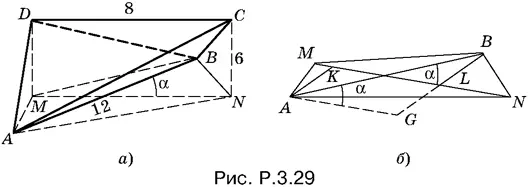
С одной стороны, его можно рассматривать как составленное из двух пирамид с общим основанием MNCD и с вершинами в точках A и B . Основание MNCD — прямоугольник с известными сторонами. Высотами будут перпендикуляры AK и BL , опущенные на MN (рис. P.3.29, б ). Так как нам нужна сумма объемов двух пирамид с общим основанием, то выразим AK + BL через AB и sin α. Тогда объем нашего тела будет выражен через α.

С другой стороны, V ANBMCD = V ABCD + V ABMD + V ABNC .

Проведем AG || KL (см. рис. P.3.29, б ). Тогда

AK + BL = GB = 12 sin α, S MNCD = 6 · 8 = 48,

V ANBMCD = ⅓ S MNCD ( AK + BL ) = 4 · 48 sin α,

S MANB = ½ AB · NM sin α = 48 sin α.

V ABCD + V ABMD + V ABNC = 48 + 6/ 3( S ABM + S ABN ) = 48 + 2 S MANB = 48 + 2 · 48 sin α.

Таким образом,

48 + 2 · 48 sin α = 4 · 48 sin α.

Отсюда

sin α = ½.

Ответ. α = π/ 6.

3.30.Поставим четырехугольную пирамиду A 1 BB 1 C 1 C , в которую вписан шар, на основание BB 1 C 1 C (рис. P.3.30). Пусть H — высота призмы, а — сторона ее основания. Радиусы окружностей с центрами O и O 1равны R . Так как треугольник B 1 A 1 C 1правильный, то а = 2√3 R .