Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

Ответ.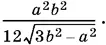

3.41.Расстояние между центрами O 1и O 3двух не касающихся друг друга шаров равно 2 r √2 (рис. P.3.41, а ).

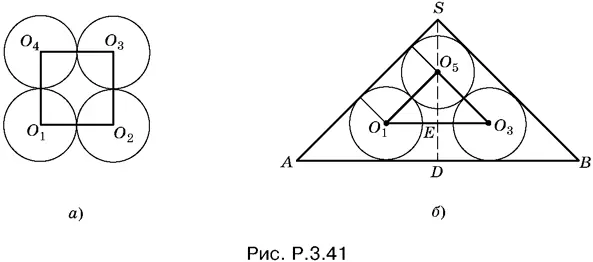
На рис. P.3.41, б изображено осевое сечение конуса, проходящее через O 1и O 3. B этом же сечении будет лежать и O 5. B треугольнике O 5 O 1 Е сторона O 1 O 5= 2 r , а O 1 Е = r √2 , следовательно 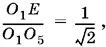т. е. угол O 5 O 1 Е равен 45°. Треугольник ASD подобен треугольнику O 1 O 5 Е . Поэтому H = R . Найдем H :

H = SO 5+ O 5 E + ED = √2 r + 2 r / √2+ r = r (2√2 + 1).

Теперь можно найти и объем конуса:

V = π r ³/ 3(2√2 + 1)³.

Ответ. π r ³/ 3(22√2 + 25).

3.42.Так как ребро SD перпендикулярно к плоскости основания, то треугольник SCD (рис. P.3.42, а ), в который вписана окружность основания цилиндра, прямоугольный.

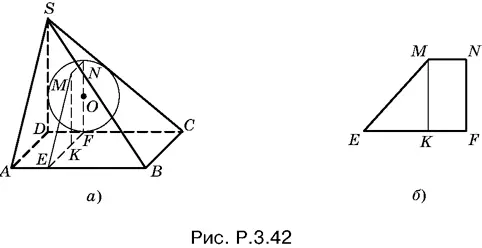
Радиус этой окружности равен частному от деления площади треугольника SDC на полупериметр, т. е.

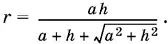
Угол MEK равен углу SAD , так как треугольники MEK и SAD подобны. Из треугольника SAD находим ctg ∠ SAD = a / h . Следовательно, и ctg ∠ MEK = a / h . Для дальнейших рассуждений достаточно рассмотреть трапецию EMNF (рис. P.3.42, б ).

Отрезок MK = 2 r . Из треугольника MEK находим

EK = MK ctg ∠ MEK = 2 ra / h .

Искомый отрезок

KF = EF − EK = a − 2 ra / h = a ( h − 2 r )/ h .

Ответ.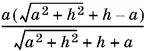

3.43.Пусть OA = R , SO = H , ребро куба равно a (рис. P.3.43).

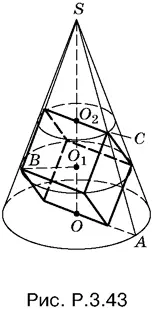
Из подобия треугольников SOA и SO 1 B получим

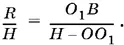
Так как

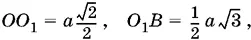
то

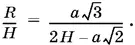
Из подобия треугольников SO 1 B и SO 2 C

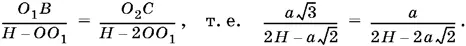
Упростим последнюю пропорцию и найдем из нее H :

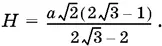
С помощью первого соотношения определим теперь R :

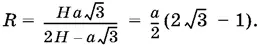
Остается сосчитать отношение объемов: π R ² H / 3 a ³.

Ответ.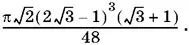

3.44.Обозначим через а сторону нижнего основания пирамиды, через b сторону ее верхнего основания, а через S площадь боковой грани. Объем пирамиды можно записать так:

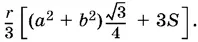
С другой стороны, объем равен

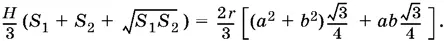
Приравнивая эти два выражения, найдем

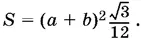
Вспомним, что боковая грань — трапеция, боковые ребра которой равны верхнему основанию. Площадь этой трапеции легко найти, если вычислить ее высоту:

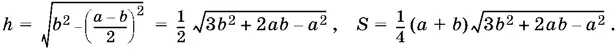
Сравнивая с предыдущим выражением для S , получим уравнение относительно а / b . После сокращения на а + b (равенство суммы а + b нулю не имеет геометрического смысла) и возведения в квадрат придем к выражению

2 b ² + ab − а ² = 0

или

( a / b )² − a / b − 2 = 0.

Так как а и b — положительные величины, то а / b = 2, или а = 2 b .

Чтобы связать величины b и r , спроецируем точку С 1на плоскость нижнего основания (рис. P.3.44). Поскольку радиус описанной окружности треугольника ABC в два раза больше радиуса описанной окружности треугольника А 1 В 1 С 1, то DC = b / √3.

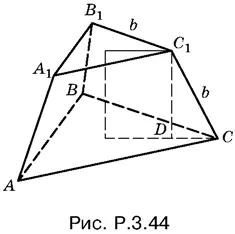
По теореме Пифагора для треугольника С 1 DС

b ² − b ²/ 3= 4 r ²,

откуда

b = r √6, а = 2 b = 2 r √6.

Остается вычислить объем:

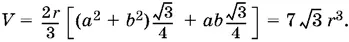
Ответ.7√3 r ³.

3.45.Пусть О 1и О 2— центры меньших шаров, О 3— центр большого шара, а О — центр шара, радиус которого нужно определить. Спроецируем точки O 1, O 2, O 3и О на плоскость (рис. P.3.45). Треугольник Р 1 Р 2 Р 3равнобедренный и точка P лежит на его медиане и высоте.

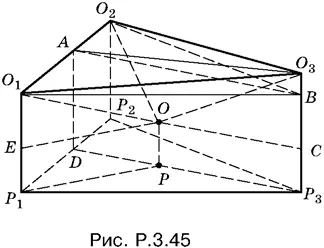
Обозначим радиус ОР = x . После этого многие отрезки на рис. P.3.45 можно будет выразить через R , r и x . Отложим на O 3 Р 3= R отрезок ВР 3= r . Треугольники O 1 O 2 В и Р 1 Р 2 Р 3равны, как основания призмы. Перед нами задачи — связать величины r = О 1 Р 1= О 2 Р 2, R = О 3 Р 3, x = ОР . Прямоугольные треугольники ОО 1 Е и ОО 3 С позволяют вычислить отрезки РР 1и Р 3 Р . Отрезок DР 3= AB можно найти из прямоугольного треугольника О 3 АВ ( О 3 А можно считать известной величиной). Полученные отрезки образуют прямоугольный треугольник P 1 DP , для которого будут вычислены все стороны. Теорема Пифагора для этого треугольника и даст нужное нам соотношение между r , R и x .