Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

Возможен еще один случай, который является как бы совпадением двух разобранных вариантов — точка О совпадает с вершиной B . Тогда призма прямая и при S 1= S 2из формулы (6) получим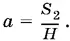

Поскольку в первом случае S 1= аВ 1 D , S 2= аВ 1 В и В 1 D < В 1 В , то первому случаю соответствует требование S 1< S 2. Условие положительности подкоренного выражения 4 S ² 1− S ² 2приводит ко второму ограничению S 2< 2 S 1.

Для второго случая получаем S 1= аВ 1 D , S 2= aH . Так как В 1 D > H , то S 1> S 2. Случай S 1= S 2можно отнести к этому случаю.

Ответ. 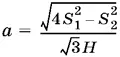при S 1< S 2< 2 S 1, а = S 2/ H при S 1 ≥ S 2.

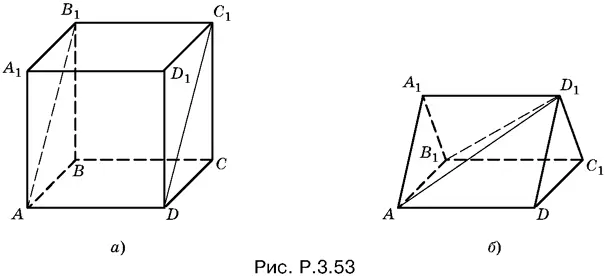
3.53.Проведем в кубе сечение AB 1 C 1 D (рис. P.3.53, а ). Оно разобьет куб на две равные треугольные призмы. Возьмем одну из призм (рис P.3.53, б ) и в качестве основания четырехугольной пирамиды выберем четырехугольник AB 1 C 1 D , а в качестве ее вершины точку D 1. Оставшаяся часть призмы ( D 1 AA 1 B 1) образует треугольную пирамиду. Аналогично разобьем и вторую призму. Поскольку четыре пирамиды заполняют весь объем куба, их суммирующий объем максимален.

3.54. Пусть O 1— центр шара, описанного около пирамиды SABC , а O — центр правильного треугольника ABC , лежащего в ее основании. Тогда O 1 O — перпендикуляр к плоскости основания (рис. P.3.54).

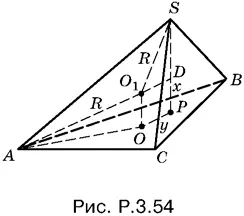
(По условию точка O 1равноудалена от A , B и C .) Обозначим длину отрезка O 1 O через x , а длину отрезка OP через y . Так как AO 1= SO 1= R , а AO = 6/ √3 = 2√3, то по теореме Пифагора для треугольника AOO 1: x ² + AO ² = R ², т. е. x ² + 12 = R ². Соотношение для y найдем из треугольника SO 1 D , где O 1 D = y , SO 1= R . Тогда SD ² = R ² − y ². Но SD есть либо 4 − x , либо 4 + x в зависимости от расположения O 1. Поэтому найдем x : x = | SP − SD |, что охватывает сразу два возможных случая и приводит к уравнению

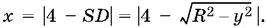
Отсюда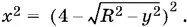

Но x ² = R ² − 12, т. е.

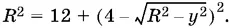
Тогда 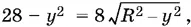а после возведения в квадрат и приведения подобных членов: 64 R ² = 28² + 8 у ² + y 4или 64 R ² = ( y ² + 4)² + (28² − 16).

Поскольку

28² − 16/ 64= 4² · 7² − 4²/ 4² · 4= 7² − 1/ 4= 48/ 4= 12,

имеем R ² = ( y ² + 4)²/ 64+ 12. Это выражение при x = 0 достигает своего минимального значения R ² = 4²/ 64+ 12 = 12¼ = 49/ 4, т.е. R = 7/ 2.

Ответ.3,5.

Замечание. Условие задачи, в силу которого основание P высоты SP пирамиды SABC принадлежит ее основанию ABC , при решении не использовано. Это условие оказалось лишним. Следовательно, в постановке задачи имеется неточность. Мы пытались использовать это условие, когда в первом указании строили прямую призму, верхнему основанию которой должна принадлежать вершина S . Эти ограничения оказались невостребованными при решении задачи. Задача реально предлагалась на вступительных экзаменах.

4.1.Проведем AE до пересечения с ОС в точке F (рис. P.4.1, а ). Точка F лежит в плоскости грани DD 1 C 1 C , в которой лежит и точка О , принадлежащая сечению. Проведем FO до пересечения с D 1 D в точке N . Таким образом, сечение, о котором идет речь в условии, построено; это ANME (см. рис. P.4.1, а ).

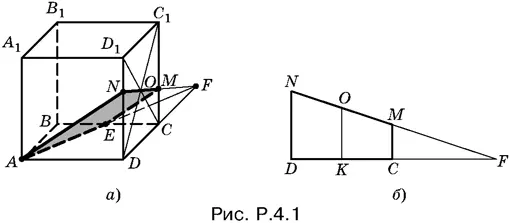
Обозначим ребро куба через а и вычислим объем фигуры, лежащей под сечением, как разность объемов двух пирамид: NAFD и MEFC .

Отрезок EC — средняя линия в треугольнике AFD , следовательно, CF = СО = а .

Вычертим отдельно треугольник BFD и проведем OK || ND (рис. P.4.1, б ). Так как О — центр грани куба, то OK = a / 2, DK = KC = а / 2. Из подобия образовавшихся треугольников находим

MC = а / 3, ND = 2 MC = 2 а / 3.

Так как треугольники EFC и EAB равны (см. рис. P.4.1, а ), то площадь треугольника AFD равна а ², а площадь треугольника EFC равна a ²/ 4. Теперь можно вычислить объем фигуры, лежащей под сечением ANME :

⅓ ND · a ² − ⅓ MC · a ²/ 4= ⅓ 2 a / 3 a ² − ⅓ a / 3 a ²/ 4= 7 a ³/ 36,

и найти искомое отношение объемов.

Ответ.29 : 7.

4.2.Проведем прямую FG , которая пересечет А 1 В 1и А 1 D 1в точках M и L соответственно (рис. P.4.2). Соединив точки M и А и точки L и А , получим еще две точки E и K , принадлежащие сечению.

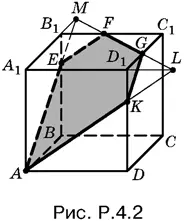
Площадь сечения AEFGK вычислим как разность площади треугольника AML и удвоенной площади треугольника KGL .

Треугольники ЕВ 1 М , FC 1 G и GD 1 L равны. Следовательно, D 1 L = В 1 F = ½, MF = FG = GL . С помощью треугольников МА 1 L и АА 1 L можно найти стороны треугольника AML :

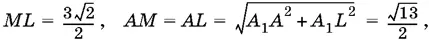
его высоту

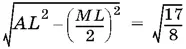
и его площадь

Треугольники AML и KGL подобны, так как GK и AM параллельны (они получены в результате пересечения двух параллельных граней куба плоскостью сечения), с коэффициентом подобия ⅓ (мы доказали раньше, что 3 GL = ML ). Следовательно, площадь треугольника KGL равна 1/ 9площади треугольника AML , а площадь сечения AEFGK равна 7/ 9площади AML .