Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы
- Название:Сборник задач по математике с решениями для поступающих в вузы
- Автор:
- Жанр:
- Издательство:«ОНИКС 21 век» «Мир и Образование»
- Год:2003
- Город:Москва
- ISBN:5-329-00766-6, 5-94666-080-2
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы краткое содержание
Основу задачника составили варианты письменных работ по математике, предлагавшихся на вступительных экзаменах в ряде ведущих вузов Москвы.
Сборник содержит около 500 типовых задач. K каждой задаче дается до трех указаний, помогающих найти правильный путь к решению, а затем приводится подробное решение.
Пособие может использоваться при самостоятельной подготовке к экзаменам в вуз, а также на подготовительных отделениях и курсах.
Сборник задач по математике с решениями для поступающих в вузы - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Спроецируем точку О 1на АО и рассмотрим прямоугольный треугольник O 1 EO 2. B нем O 1 O 2равно разности радиусов, т. е. O 1 O 2= a / 2− r ; EO 1равно половине OB , т. е. EO 1= а √3/ 6. Отрезок O 2 Е = | AE − AO 2|. Знак абсолютной величины означает, что точка О 2может оказаться ниже точки E , либо выше ее (см. рис. P.3.49, на котором изображены оба случая). Так как AE = ½, АО = a / √6, а AO 2= 3 r , то O 2 E = | a / √6− 3 r |.
По теореме Пифагора O 2 O ² 1= O 2 Е ² + EO ² 1, т. е.
( a / 2− r )² = ( a / √6− 3 r )² + a ²/ 12.
После простых преобразований получим уравнение
8 r ² + (1 − √6) ar = 0,
откуда
r = √6 − 1/ 8 а .
Так как АO 2= 3 r , то AO2 = 3√6 − 1/ 8 а , в то время как AE = a / √6.
Сравнивая AO 2и AE , мы видим, что AO 2больше. Следовательно, точка O 2на рис. P.3.49 должна располагаться ниже точки E .
Ответ. √6 − 1/ 8 а .
3.50.Плоскость Π, проходящая через ось РР и центр О основания пирамиды, образует в сечении некоторый треугольник SMN (рис. P.3.50). Повернем треугольник SAB около оси РР так, чтобы он лег в плоскость Π. Так как AB = MN , а высота SO меньше высоты SK , то треугольники расположатся так, как показано на рис. P.3.50. Любое другое сечение SEF пирамиды попадет внутрь пятиугольника SMABN , а все сечения дважды покроют этот пятиугольник.
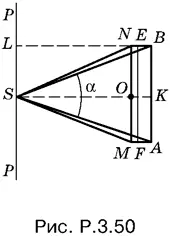
Остается определить объем тела, полученного от вращения пятиугольника SMABN вокруг оси РР . Половину искомого объема можно получить в виде разности объемов цилиндра, полученного от вращения прямоугольника SKBL , и конуса, полученного от вращения треугольника SNL :
½ V SMABN = V SKBL − V SNL = π SK ² · BK − ⅓π LN ² · BK = π BK ( SK ² − ⅓ LN ²).
Из соответствующих треугольников находим
SK = a / 2ctg α/ 2; LN ² = SO ² = SN ² − NO ² = a ²/ 4ctg² α/ 2− a ²/ 4.
Таким образом,
V SMABN = π a ( a ²/ 4ctg² α/ 2− ⅓ a ²/ 4ctg² α/ 2+ a ²/ 12) = π a ³/ 12(2 ctg² α/ 2+1).
Ответ. π a ³/ 12(2 ctg² α/ 2+1).
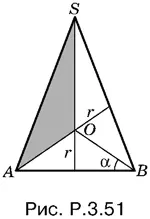
3.51. Способ 1.Рассмотрим радиус r вписанного в конус шара и угол α (на рис. P.3.51 изображено осевое сечение конуса).
Тогда полная поверхность конуса будет равна
S пк= π R ( R + l ) = π r ² ctg² α (1 + 1/ cos 2α),
где радиус R основания конуса и его образующая l равны соответственно
R = r ctg α, l = r ctg α/ cos 2α.
(промежуточные выкладки проделайте самостоятельно). Так как S ш= 4π r ² и по условию S пк= 2 S ш, то после сокращения на π r ² и несложных преобразований приходим к тригонометрическому уравнению
1 + cos 2α/ cos 2α= 8 tg² α.
Выразив tg² α через cos 2α, получим
1 + cos 2α/ cos 2α= 8 1 − cos 2α/ cos 2α,
откуда cos 2α = ⅓.
Найдем теперь требуемое отношение объемов. Имеем
V к= π r ³/ 3ctg³ α tg 2α, V ш= 4/ 3π r ³.
Преобразуем выражение ctg³ α tg 2α, имея в виду, что cos 2α = ⅓:
ctg³ α tg 2α = ctg² α · ctg α sin 2α/ cos 2α= 1 + cos 2α/ 1 − cos 2α· cos α · 2 sin α cos α/ ⅓ sin α= 8.
Следовательно, V к= 2 V ш, т. е. отношение объема конуса к объему шара равно 2.
Способ 2.Представим объем конуса как сумму двух объемов V 1и V 2, где V 1— объем тела, образуемого вращением заштрихованного на рис. P.3.51 треугольника вокруг оси конуса, а V 2— объем конуса с осевым сечением AOB . Имеем
V к= V 1+ V 2= ⅓ rS б+ ⅓ rS o= r / 3( S б+ S o) = r / 3 S пк
(здесь использована лемма об объеме тела вращения треугольника; S o— площадь основания конуса, S б— площадь его боковой поверхности).
Так как V ш= r / 3(4π r ³) = r / 3 S ш, то
V к: V ш= ( r / 3 S пк) : ( r / 3 S ш) = 2.
Ответ.Отношение объемов равно 2.
3.52.Предположим, что двум равновеликим граням принадлежит ребро BB 1. Спроецируем точку B 1на плоскость основания и обозначим проекцию буквой O . Если B 1 E и B 1 D — соответственно высоты параллелограммов CC 1 B 1 B и AA 1 B 1 B , то B 1 D = B 1 E , поскольку площади и основания у этих параллелограммов равны. Следовательно, прямоугольные треугольники B 1 OE и B 1 OD равны, т. е. точка O находится на одинаковом расстоянии от прямых AB и CB . Поэтому (подробнее см. задачу 5.4) она лежит на биссектрисе одного из углов, образованных этими прямыми. Случаю, когда точка O находится либо внутри угла ABC , либо попадает в угол, вертикальный по отношению к углу ABC , отвечает рис. P.3.52, а . Другой возможный вариант изображен на рис. P.3.52, б . Здесь в построении участвует биссектриса угла ABN .
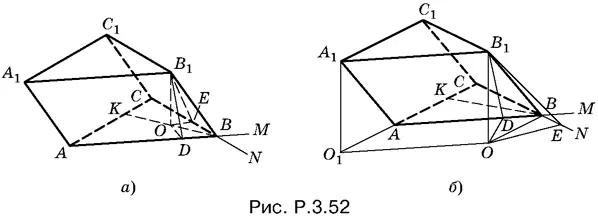
Начнем с первого случая. Так как ABC — правильный треугольник, то BK ⊥ AC и, следовательно, В 1 В ⊥ AC . Поскольку ребро A 1 A параллельно В 1 В , то А 1 A ⊥ AC . Мы доказали, что в первой из двух различных ситуаций АА 1 С 1 С — прямоугольник. Если AB = а , A 1 A = b, то S 2= ab . Чтобы связать введенные элементы с известными из условия задачи, вспомним, что треугольник, лежащий в основании, правильный. Следовательно, OB = 2 · OD (угол OBD равен π/ 6). Отрезок OD найдем из треугольника В 1 OD , а отрезок OB — из треугольника В 1 OB .
Итак,
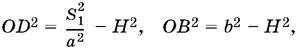
благодаря чему
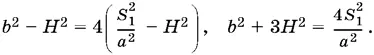
Поскольку 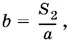 получаем возможность определить а :
получаем возможность определить а :
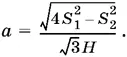
(6)
Рассмотрим теперь второй из возможных случаев (см. рис. P.3.52, б ). Теперь ВО и AC параллельны и ВО ⊥ KB . Поэтому KB ⊥ ВВ 1и, следовательно, KB ⊥ АА 1. Мы установили, что параллелограмм АА 1 С 1 С лежит во втором случае в плоскости, перпендикулярной к плоскости основания призмы. Следовательно, высота А 1 O 1призмы принадлежит плоскости АА 1 С 1 С , т. е. Ha = S 2, откуда 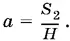
Интервал:
Закладка:










