Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

Перенесем теперь плоскость P параллельно так, чтобы четырехугольник уперся в нее одной из своих вершин, которую обозначим буквой А (рис. P.3.36, б ).

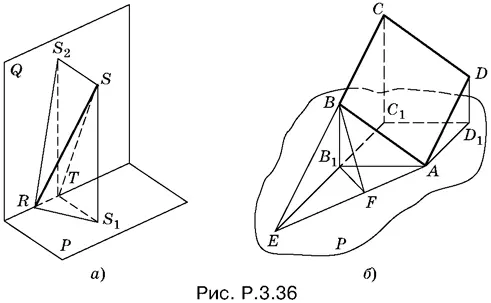
Спроецируем четырехугольник ABCD на плоскость P . Поскольку его проекция АВ 1 С 1 D 1— квадрат, то ABCD — параллелограмм. Поэтому один из отрезков AB или AD равен √5/ 2. Предположим, что это AB .

Построим теперь след, оставленный плоскостью четырехугольника ABCD на плоскости P . Для этого построим вначале точку E , в которой пересекаются прямые BC и В 1 С 1, а затем соединим E и А . Угол между плоскостями ABCD и P измерим линейным углом BFB 1, равным 45°. Остается провести вычисления: 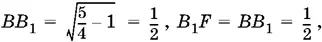следовательно, угол B 1 AF равен 30° и поэтому B 1 E = 1/ √3; находим 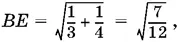и так как 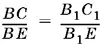, то BC = √7/ 2.

Ответ.√5 + √7 .

3.37.Опишем около данной пирамиды конус с образующей l , высотой H и радиусом нижнего основания R . Объем конуса больше объема пирамиды. Если мы докажем, что объем конуса меньше куба образующей, то задача тем самым будет решена.

Рассмотрим угол α между H и l . Тогда

H = l cos α, R = l sin α,

а объем конуса равен

V = π/ 3 R ² H = π/ 3 l ³ sin² α cos α.

Составим отношение:

V / l ³= ⅓π sin² α cos α = π/ 6sin 2α sin α ≤ π/ 6< 1,

что и доказывает сформулированное в условии утверждение.

3.38.B осевом сечении конуса получим картину, изображенную на рис. P.3.38.

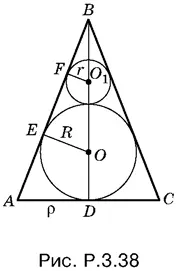
По условию r = pR . Из подобия треугольников ЕОВ и FO 1 B получим

r / R = H − 2 R − r / H − R , т. е. H = 2 R ²/ R − r ,

а из подобия треугольников AOB и ОЕВ ( AB = l ) найдем

l / ρ= H − R / R , (5)

т. е.

l = ρ H − R / R = ρ 1 + p / 1 − p .

Так как l ² − ρ² = Н ², получаем уравнение относительно ρ, решая которое находим ρ² = R ²/ p . Полная поверхность конуса равна π p (ρ + 1). С помощью производной пропорции из соотношения (5) получим

l + ρ/ ρ= H / ρ, т. е. ( l + ρ)ρ = ρ² H / R = 2 R ²/ p (1 − p ).

Сумма поверхностей шаров равна 4π( R ² + r ²).

Составим искомое отношение:

2( R ² + r ²) p ( p − 1)/ R ²= 2(1 + p ²) p (1 − p ).

Ответ.2 p (1 − p )(1 + p ²).

3.39. Обозначим радиус сферы через R и рассмотрим осевое сечение каждого из конусов. Второй конус можно расположить внутри сферы произвольным образом. Мы расположим его так, чтобы образующие обоих конусов были параллельны (рис. P.3.39). Выразим радиусы оснований конусов через R .

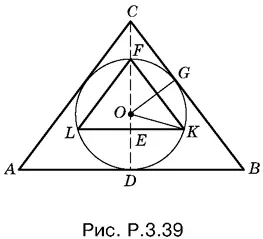
B треугольнике FOK углы OFK и OKF равны α/ 2· Следовательно, угол EOK равен их сумме, т. е. α. Из треугольника EOK находим EK = R sin α. Далее,

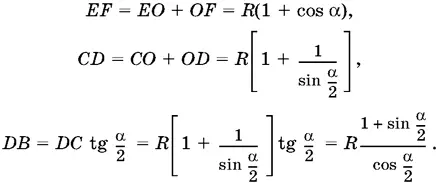
Составим теперь отношение объемов и приравняем его к a . После простых преобразований придем к уравнению относительно α:

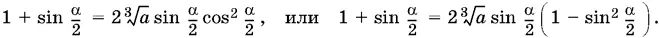
Так как 1 + sin α/ 2 ≠ 0 (иначе не существует конус), то

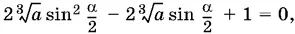
откуда

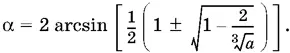
Чтобы можно было осуществить извлечение корня, необходимо взять а ≥ 8.

Так как а > 0, то выражение, стоящее под знаком арксинуса, как легко проверить, всегда расположено между 0 и 1.

Ответ.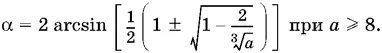

3.40.Так как O 1— центр сферы, касающейся граней SAB и SAC в точках B и C (рис. P.3.40, а ), то O 1лежит в плоскости, перпендикулярной к их общему ребру SA и проходящей через эти точки. При этом ED — биссектриса линейного угла ВЕС , измеряющего двугранный угол между рассматриваемыми плоскостями.

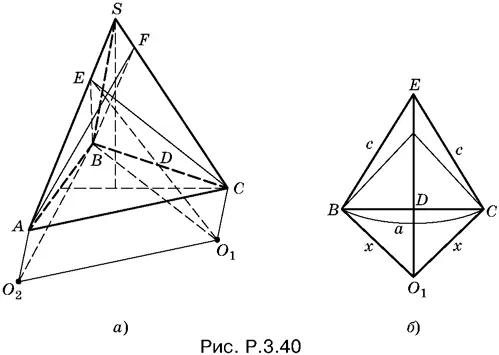
Если сделать такие же построения для второй сферы O 2, то получим четырехугольник AFBO 2, равный четырехугольнику BECO 1(равенство очевидно из соображений симметрии, однако этот факт легко устанавливается и непосредственно). Следовательно, CO 1= AO 2= BO 2= BO 1. Заметим, что AO || CO 1как два перпендикуляра к плоскости ASC . Итак, O 1 O 2= AC = а .

Поскольку O 1 B ⊥ ASB , то O 1 B ⊥ SB , аналогично O 2 B ⊥ SB , откуда SB ⊥ O 1 BO 2. Мы доказали, что SB — высота пирамиды SO 1 BO 2.

Чтобы ответить на поставленный в задаче вопрос, остается вычислить длину отрезка BO 1. Так как отрезок EC из треугольника ASC определяется легко:

EC ² = a ²/ 4 b ²(4 b ² − a ²),

то дальнейшие вычисления нельзя проводить, оставаясь в плоскости BEC (рис. P.3.40, б ). Обратим лишь внимание на тот факт, что треугольники BES и CES равны, т. е. BE = CE , откуда следует, что биссектриса ED является в треугольнике BEC и медианой. Фигура BECO 1— ромбоид ( BC ⊥ EO 1). Обозначим EC = с , BO 1= x . Треугольники ECO 1и ECD подобны. Поэтому ED : с = a / 2: x , откуда x = ac / 2 ED , т. е. x ² = a ² c ²/ 4 c ² − a ².

Подставляя вместо с = EC его выражение через а и b , получим

OB ² = a ²(4 b ² − a ²)/ 4(3 b ² − a ²).

Теперь можно определить высоту треугольника O 1 BO 2, опущенную на O 1 O 2. Она равна 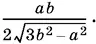Все элементы, необходимые для вычисления объема, сосчитаны.