Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы
- Название:Сборник задач по математике с решениями для поступающих в вузы
- Автор:
- Жанр:
- Издательство:«ОНИКС 21 век» «Мир и Образование»
- Год:2003
- Город:Москва
- ISBN:5-329-00766-6, 5-94666-080-2
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы краткое содержание
Основу задачника составили варианты письменных работ по математике, предлагавшихся на вступительных экзаменах в ряде ведущих вузов Москвы.
Сборник содержит около 500 типовых задач. K каждой задаче дается до трех указаний, помогающих найти правильный путь к решению, а затем приводится подробное решение.
Пособие может использоваться при самостоятельной подготовке к экзаменам в вуз, а также на подготовительных отделениях и курсах.
Сборник задач по математике с решениями для поступающих в вузы - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
OK ² = OM ² − m ², OK ² = OP ² − l ², т. е. OM ² − m ² = OP ² − l ²
(через m и l обозначены длины отрезков MK и KP соответственно).
Так как OM ² = а ² + AO ², а OP ² = b ² + OB ² и AO = OB , то
а ² − m ² = b ² − l ²
или
m ² − l ² = а ² − b ². (1)
Точно так же приравняем выражения для отрезка AP ², полученные из треугольников MAP и ABP :
( m + l )² − а ² = b ² + AB ².
Вспомнив, что по условию AB ² = 2 ab , получим ( m + l )² = а ² + 2 ab + b ², т. е.
m + l = а + b . (2)
Разделив почленно равенство (1) на равенство (2), получим
m − l = а − b , (3)
а решая систему из уравнений (2) и (3), найдем m = а , b = l , что и требовалось доказать.
3.7.Обозначим через PQ (рис. P.3.7) прямую, по которой пересекаются грани AOD и BOC , а через RS — прямую, по которой пересекаются грани AOB и DOC . Прямые PQ и RS определяют плоскость P . Через произвольную точку M на АО проведем плоскость, параллельную плоскости P . Фигура MNKL , получившаяся в сечении, будет параллелограммом.
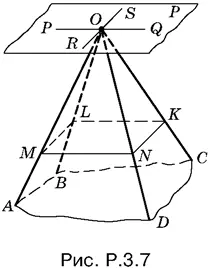
B самом деле, MN || PQ и LK || PQ , a ML || RS и NK || RS , как прямые, получившиеся в результате пересечения двух параллельных плоскостей третьей. Следовательно, MN || LK и ML || NK , что и требовалось доказать.
3.8.Продолжим ED и CB (рис. P.3.8) до пересечения в точке F и проведем AF — ребро двугранного угла, косинус которого нужно найти.
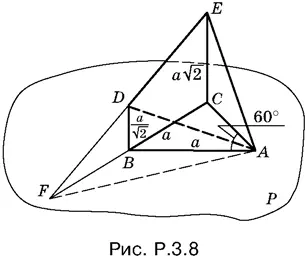
Так как EC = 2 DB (по условию), то DB — средняя линия в треугольнике EFC . Поэтому FB = BC = а . Поскольку BA = а , то треугольник FBA равнобедренный. Сумма его углов, прилежавших к FA , равна 60°, а угол BAF равен 30°.
Мы убедились в том, что угол CAF прямой, а следовательно, линейный угол EAC измеряет искомый двугранный угол. Теперь остаются простые вычисления:

По теореме о трех перпендикулярах отрезки EA и FA взаимно перпендикулярны; поэтому площадь треугольника EAF равна ½ EA · AF , где AF = а √3 . Итак, площадь треугольника AFE равна 3 a ²/ 2, и вследствие того, что FD = DE , площадь треугольника DEA в два раза меньше.
Ответ. 3 a ²/ 2, 1/ √3.
3.9.Обозначим высоту SO пирамиды через H . Предположим, что вершина пирамиды спроецируется в точку O , лежащую внутри треугольника ABC , и пусть углы SDO , SEO и SFO измеряют данные двугранные углы (рис. P.3.9, а ).
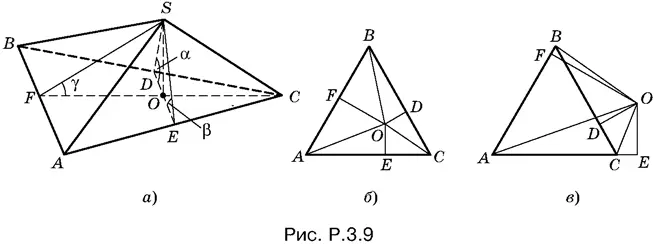
Рассмотрим отдельно треугольник ABC (рис. P.3.9, б ). Площадь его, с одной стороны, равна сумме площадей треугольников AOB , BOC и COA , а с другой стороны, равна a ²√3/ 4. Поэтому
½ a ( OF + OD + OE ) = a ²√3/ 4, т.е. OF + OD + OE = a √3/ 2.
Каждый из отрезков OF , OD и OE можно выразить через H :
OD = H ctg α, OE = H ctg β, OF = H ctg γ. Следовательно,
H = a √3/ 2(ctg α + ctg β + ctg γ).
Если точка О лежит вне треугольника ABC , то один из данных двугранных углов тупой (на рис. P.3.9, в угол при BC , т. е. α). Следовательно, его котангенс будет отрицательным. Это соответствует тому факту, что площадь треугольника ABC равна сумме площадей треугольников АВО и АОС за вычетом площади треугольника ВОС . Таким образом, результат останется таким же, как в случае, когда О лежит внутри треугольника ABC .
Наконец, как легко убедиться, полученная формула дает верный результат и в том случае, когда точка О лежит на стороне треугольника ABC или совпадает с его вершиной. (Соответствующие котангенсы обращаются в нуль.)
Ответ. V = a ³/ 8(ctg α + ctg β + ctg γ).
3.10.Так как AC = BC по условию (рис. P.3.10), то прямоугольные треугольники ADC и BDC равны и, следовательно, AD = BD . Треугольник ADB — равнобедренный, его медиана DE , проведенная из вершины D , будет одновременно и высотой. Таким образом, мы доказали, что двугранный угол при ребре AB измеряется линейным углом DEC , который обозначим через x .
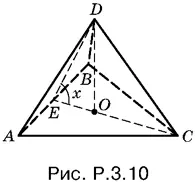
Высота DO треугольника EDC будет высотой пирамиды. B самом деле, ребро AB перпендикулярно к ED и EP , т. е. к плоскости EDC . Отрезок DO , следовательно, перпендикулярен не только к EC , но и к AB , т. е. перпендикулярен к плоскости ABC .
Заметим также, что CD — перпендикуляр к плоскости ADB , а поэтому треугольник EDC прямоугольный с прямым углом при вершине D .
Мы знаем, что V = ⅓ S · OD . Отрезок OD равен ED sin x , а отрезок ED в свою очередь равен EC cos x , т. е. 2 S / a cos x .
Итак,
V = ⅓ S · 2 S / a cos x sin x ,
откуда sin 2 x = 3 Va / S ².
Чтобы найти x , заметим, что угол x острый.
Ответ.½acrsin 3 aV / S ².
3.11.Так как площадь основания равна √3, то сторона основания равна 2. Из треугольника AOS (рис. P.3.11) находим AO = b cos x ; с другой стороны,
AO = ⅔ AD = ⅔ a √3/ 2.
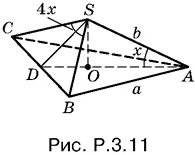
Поэтому
a / √3= b cos x .
Из треугольника CDS находим CD = a / 2= b sin 2 x . Разделив второе соотношение на первое, получим
sin x = √3/ 4.
Так как SD = a / 2ctg 2 x , то нужно вычислить ctg 2 x :
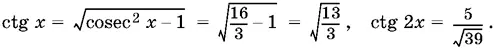
Следовательно, SD = 5/ √39, а площадь боковой поверхности равна 3/ 2 а · SD .
Ответ. 5/ √39.
3.12.На рис. P.3.12 треугольники AEC и С 1 ЕА 1подобны, так как медианы AE и СЕ делятся точками C 1и A 1в одинаковом отношении 2:1.
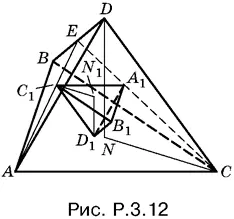
Поэтому C 1 A 1= ⅓ AC . Аналогично доказывается, что В 1 А 1= ⅓ AB и C 1 B 1= ⅓ BC и т. д., т. е. площади S 1и S оснований пирамиды относятся как 1 : 9. Подобные треугольники ABC и A 1 B 1 C 1лежат в параллельных плоскостях, так как их стороны параллельны. Следовательно, высоты DN и D 1 N 1, проведенные в тетраэдрах, параллельны и прямоугольные треугольники DNC и D 1 N 1 C 1подобны, т. е. D 1 N 1= ⅓ DN . Остается сравнить объемы 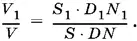
Интервал:
Закладка:










