Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

Четырехугольник ADEC искомый. (Сделайте рисунок для случая, когда угол B тупой.)

Докажите, что в обоих случаях задача имеет единственное решение.

2.7.Проведем через точку M прямую AB так, чтобы ее отрезок, заключенный между сторонами угла, делился в точке M пополам. Для этого построим МС параллельно OA (рис. P.2.7, а) и отложим СВ = ОС . Так как СМ — средняя линия в треугольнике ОВА , то ВМ = МА .

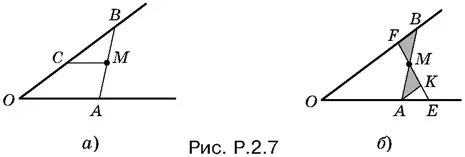
Итак, пусть AM = МВ (рис. P.2.7, б ). Проведем произвольную прямую EF через точку M . Покажем, что площадь треугольника ОАВ меньше площади треугольника ОЕF . Проведем AK параллельно OB (если FM < ЕМ). Треугольники AMK и ВМF равны. Следовательно,

S ОЕf = S ОАМF + S AMK + S AEK > S ОАМF + S ВМF = S ОАВ .

2.8.Вместо искомого треугольника ABC построим треугольник А 1 АА 2, который получается из ABC так, как показано на рис. P.2.8 ( А 1 В = ВА , А 2 С = СА ).

Угол А 1 АА 2этого треугольника равен α + β + А . Однако 2α = B , а 2β = С (по свойству внешних углов). Поэтому

α + β + А = B + C / 2+ A = π − A / 2+ A = π + A / 2.

Теперь в треугольнике А 1 АА 2известны основание А 1 А 2= 2 p , высота, равная h а , и угол при вершине, равный π/ 2 + А / 2. Вершина А будет лежать на пересечении прямой, параллельной А 1 А 2и отстоящей от А 1 А 2на расстоянии h а , и сегмента, построенного на отрезке А 1 А 2и вмещающего угол π/ 2+ А / 2.

Вершины B и С лежат на пересечении А 1 А 2и перпендикуляров, проведенных через середины А 1 А и А 2 А .

Задача может иметь два симметричных решения, если высота меньше стрелки сегмента, одно решение, если они равны, и не имеет решений, если h а больше стрелки сегмента.

2.9.Пусть P — искомая точка. Повернем треугольник АВР на 60° вокруг точки А . При этом точка P перейдет в точку Р 1, а точка B — в точку В 1(рис. P.2.9).

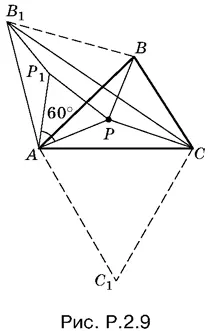
Так как угол Р 1 АР равен 60° и АР 1= АР , то треугольник Р 1 АР правильный и АР = Р 1 Р . Таким образом, В 1 Р 1 РС — ломаная, составленная из отрезков длины BP , АР и CP соответственно. Так как эта ломаная имеет закрепленные концы в точках В 1и С , то ее длина будет наименьшей, если она выпрямится в отрезок В 1 С .

Итак, точка P лежит на отрезке В 1 С . Аналогично можно показать, что точка P лежит на отрезке С 1 В , вершина С 1которого получена поворотом AC вокруг А на 60°.

Отсюда простое построение. На отрезках AB и AC строим правильные треугольники АВ 1 В и АС 1 С , лежащие вне треугольника ABC . Искомая точка P будет лежать на пересечении прямых В 1 С и С 1 В .

2.10.Если треугольник ABC искомый (рис. P.2.10), то описанная около него окружность пересечется с биссектрисой CD в точке E , делящей дугу АЕВ пополам. Следовательно, точку E мы можем построить.

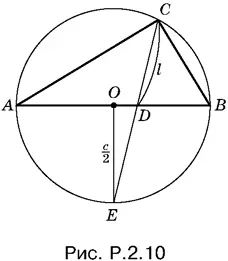
Вычислим отрезок DE . По свойству пересекающихся хорд в круге имеем CD · DE = AD · DB , или

l · DE = ( АО + DO )( OB − OD ),

т. е.

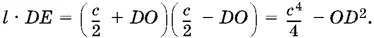
Так как OD ² = DE ² − c ²/ 4, то получаем уравнение относительно DE :

l · DE = c ²/ 2 − DE ².

Решая его, найдем

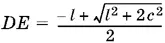
(отрицательное значение для DE не имеет геометрического смысла).

Полученная формула позволяет легко построить отрезок DE , а следовательно, и СЕ .

Задача имеет два симметричных решения, если l < c / 2, одно решение, если l = c / 2, и не имеет решений, если l > c / 2.

2.11.B произвольно выбранных точках А и E прямой MN (рис. P.2.11) строим углы BAN и FEM , равные соответственно α и β.

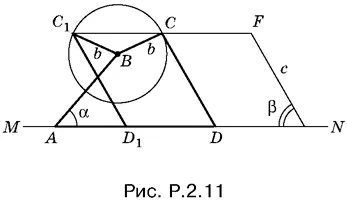
Откладываем AB = а и FE = с . Вершина С искомого четырехугольника лежит на окружности радиусом b с центром в точке B в на прямой CF параллельной MN. Если прямая пересекает окружность в двух точках С и С 1(это происходит при b > | с sin β − а sin α|), то задача имеет два различных решения: ABCD и ABC 1 D 1( CD и C 1 D 1|| EF ), причем один четырехугольник будет самопересекающимся. При b = | с sin β − а sin α| решение единственно, а при b < | с sin β − а sin α| искомый четырехугольник не существует.

2.12.На отрезке ОМ (рис. P.2.12) строим треугольник OCM , сторона OC которого равна 2 R , а сторона CM равна R . Точку пересечения OC с окружностью обозначим через B . Секущая AM — искомая.

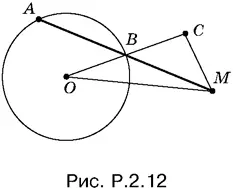
Задача имеет два решения, если MO < 3 R , одно решение, если MO = 3 R , и не имеет решений, если MO > 3 R .

2.13.Соединим центры О и О 1данных окружностей и построим на ОО 1, как на гипотенузе, прямоугольный треугольник ОЕО 1, один из катетов которого ( EO 1) равен а / 2. Через точку M пересечения окружностей, лежащую по ту же сторону от ОО 1что и построенный прямоугольный треугольник, проводим прямую, параллельную катету длины а / 2. Отрезок AB (рис. P.2.13) будет искомым.

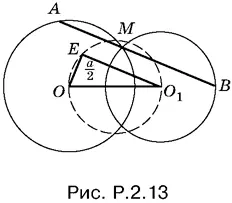
Задача имеет четыре решения, если а / 2< ОО 1, два решения, если а / 2= ОО 1, и не имеет решений, если а / 2> ОО 1.

2.14.Проводим через точку M окружность, концентрическую данной. На этой окружности строим хорду длины а , проходящую через точку M . Задача может иметь два или одно решение ( а < 2 МО ), а может и не иметь решения вовсе ( а > 2 МО ).