Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

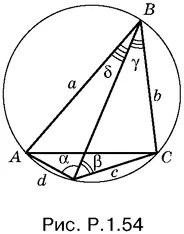
Тогда площадь S четырехугольника ABCD равна:

S = ½ ab sin (γ + δ) + ½ cd sin (α + β) = ½ sin (α + β)( ab + cd ).

(Так как γ + δ = π − (α + β), то sin (α + β) = sin (α + β).)

По теореме синусов

а = 2 R sin α = 2 sin α (так как R = 1),

b = 2 sin β, с = 2 sin γ, d = 2 sin δ.

Поэтому

S = sin (α + β)(2 sin α sin β + 2 sin γ sin δ) = sin (α + β) [cos (α − β) − cos (α + β) + cos (γ − δ) − cos (γ + δ)] =

(мы учли, что cos (α + β) = cos π − (γ + δ)) = − cos(γ + δ))

= 2 sin (α + β) cos (α + γ) − (β + δ)/ 2cos (α + δ) − (β + γ)/ 2=

(сумма четырех углов равна π, т. е. α + γ = π − (β + δ), α + δ = π − (β + γ))

= 2 sin (α + β) sin (β + δ) sin (β + γ).

Наибольшее значение S достигается при sin (β + δ) = 1, sin (β + γ) = 1 и при максимально возможном значении sin (α + β). Проверим, не противоречивы ли эти требования и реализуются ли они в реальности.

Из равенства синусов единице получаем, что β + δ = 90°, β + γ = 90°.

Отсюда δ = γ и ∠ BCD = 180 ° − (β + γ) = 90°.

Таким образом, треугольник BCD — прямоугольный, a BD — диаметр окружности и BD = 2. Далее треугольник BAD равен треугольнику BCD (δ = γ и общая гипотенуза BD ). Мы убедились, что условия sin (β + δ) = 1 и sin (β + γ) = 1 реализуемы. Остается еще одна степень свободы — выбор величины угла ABC , равного δ + γ, который по условию не превышает 45°. Чем больше угол δ + γ, тем больше sin (δ + γ) = sin (α + β). Поэтому наибольшему значению площади соответствует sin (α + β) = sin 45° = √2/ 2, т. е. S = 2 √2/ 2= √2.

Ответ. √2.

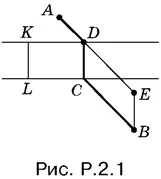
2.1.Осуществим параллельный перенос отрезка KL (рис. P.2.1), равного ширине реки, так, чтобы его точка L совпала с точкой B . Получим отрезок BE . Точку E соединим с точкой A , получим точку D , которую выберем за начало моста. Путь ADCB из A в B кратчайший, так как величина отрезка CD постоянна, а отрезки AD и CB спрямлены в AE .

2.2.На отрезках MP и PN (рис. P.2.2) построим сегменты, вмещающие угол 30°. B пересечении получим точку А . Соединим точку А с M и N , на AM и AN отложим отрезки длины а . Треугольник ABC искомый.

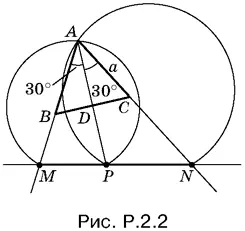
Задача имеет два решения. Одно изображено на рис. P.2.2, второе получится симметричным отражением первого от оси MN .

2.3.Пусть треугольник ABC искомый (рис. P.2.3). Отразим его от вертикальной оси, проходящей через середину BC . После этого треугольник CA 1 A отразим от оси A 1 A . B четырехугольнике C 1 ABA 1противоположные стороны AB и C 1 A 1, а также A 1 B и C 1 A равны, т. е. он — параллелограмм с углом φ при вершине C 1и углом π − φ при вершине А 1.

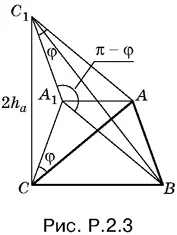
Так как точка С 1отстоит от С на расстоянии 2 h а , то треугольник СС 1 В легко построить. Остается найти точку А 1как пересечение дуги сегмента, вмещающего угол π − φ и построенного на отрезке С 1 В , с прямой, параллельной СВ и отстоящей от СВ на расстоянии h а .

Задача имеет два симметричных решения, так как дуга сегмента может быть построена в любую сторону от С 1 В . Построение возможно при любом соотношении между а , h а и 0 < φ < π.

2.4.Пусть треугольник ABC — искомый и О — центр вписанной в него окружности. Если на отрезке АО = R (рис. P.2.4), как на диаметре, построить окружность, то она пересечет стороны AC и AB в точках F и E , являющихся серединами AC и AB соответственно. Отсюда построение: на отрезке АО = R строим, как на диаметре, окружность. Из точки А раствором циркуля, равным b / 2, делаем на окружности засечку в точке F . Продолжаем AF за точку F на расстояние b / 2и получаем точку С . Из нее проводим дугу радиусом m c .

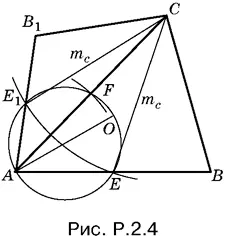
Задача имеет два решения: треугольник ABC и треугольник AB′С , если дуга ЕЕ′ пересекает окружность, построенную на AO ; одно решение, если дуга касается окружности, и не имеет решения, если общих точек у дуги и окружности нет.

2.5.Так как углы OBO 1и OCO 1(рис. P.2.5) прямые, то вершины B и С треугольника лежат на окружности, построенной на отрезке ОО 1, как на диаметре. Центр этой окружности обозначим буквой Q .

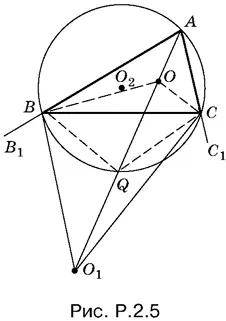
Угол BQC — центральный в той окружности, в которую угол BOC вписан (см. рисунок). Дуга, на которую опирается угол BOC , равна 2π − ∠ BQC , а так как вписанный угол измеряется половиной дуги, на которую он опирается, то

∠ ВОС = 2π − 2 ∠ ВОС .

Остается найти угол ВОС :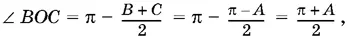

∠ ВОС = π − B + C / 2= π − π − A / 2= π + A / 2,

следовательно,

∠ BQC = 2π − (π + А ) = π − А .

Углы ВАС и BQC дают в сумме π; то же самое можно сказать об углах QBA и QCA , так как сумма всех углов четырехугольника равна 2π. Тем самым мы доказали, что точка Q лежит на окружности, описанной около треугольника ABC .

Построение можно провести следующим образом. Строим на отрезке ОО 1, как на диаметре, окружность с центром в точке Q . Радиусом О 2 Q ( О 2— центр описанной окружности) проводим окружность с центром в точке О 2. B пересечении этих окружностей получим вершины B и С искомого треугольника.

Если точка О 2лежит вне окружности радиуса, равного ¼ ОО 1, с центром Q , то задача имеет единственное решение. B противном случае решения нет. (Докажите.)

2.6.Отбросим на время условие, в силу которого точка E лежит на BC , а остальные условия сохраним. Отложим на AB произвольный отрезок AF (рис. P.2.6), а на BC — отрезок CK = AF . Через точку K проведем прямую, параллельную AC , и из точки N раствором циркуля, равным AF , сделаем на этой прямой засечку.

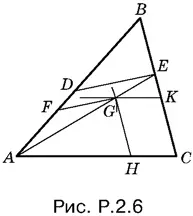
Фигура AFGH , где отрезок GH параллелен KC , будет подобна искомой с центром подобия в точке А . Строим вершину E , которая должна лежать на пересечении прямых BC и АG . Проводим DE параллельно FG .