Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

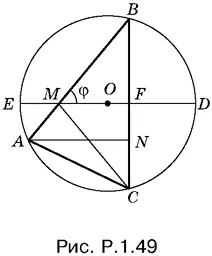
Так как диаметр ED перпендикулярен к BC , то точка N делит хорду BC пополам. Это означает, что треугольник МСВ равнобедренный. Обозначим МВ = МС = px . Угол АМС равен удвоенному углу МBC , т. е. π − 2φ. Из треугольника АМС по теореме косинусов имеем

AC ² = АМ ² + МС ² − 2 АМ · МС cos (π − 2φ) = x ²( q ² + р ² + 2 pq cos 2φ),

а из треугольника ABC по теореме синусов

AC = 2 R sin π/ 2− φ = 2 R cos φ,

т. е.

АС ² = 4 R ² cos² φ.

Приравнивая найденные выражения для АС ², получим

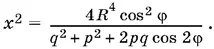
Площадь треугольника ABC будем искать в виде S = ½ AN · BC . Так как МВ = px , а МА = qx , то AB = ( p + q ) x . Из треугольника ABN находим AN = AB cos φ = ( p + q ) x cos φ. Сторону BC можно определить из треугольника MBF в котором сторона BF = ½ BC :

BC = 2 BF = 2 MB sin φ = 2 px sin φ.

Таким образом, S = p ( p + q ) x ² sin φ cos φ = ½ p ( p + q ) x ² sin 2φ, откуда

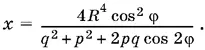
Ответ.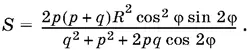

1.50.Стороны треугольника по условию равны а − d , а , а + d , где через а мы обозначили длину средней стороны. Тогда полупериметр p = 3 a / 2и из формулы Герона получим уравнение относительно а :

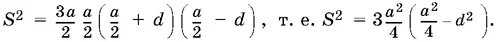
Введем новую переменную 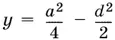. Тогда получим

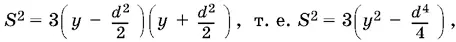
откуда

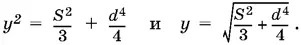
Далее найдем

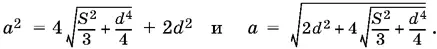
Поскольку R = abc / 4 S , то в нашем случае

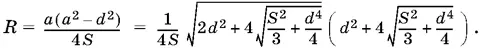
Ответ.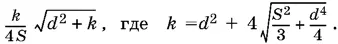

1.51.Проведем PP 1|| AC и QQ 1|| AC (рис. P.1.51).

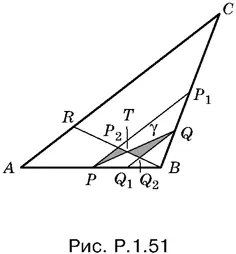
Пусть P 2— точка пересечения PP 1с BR , а Q 2— точка пересечения QQ 1с BR . По условию P — середина AB . Следовательно, Р 1— середина BC , а Р 2— середина BR. Аналогично Q — середина P 1 B (так как по условию QB = BC / 4), Q 1— середина PB , Q 2— середина BP 2. Из подобия треугольников P 2 TP и Q 2 TQ (у них равны углы) следует, что P 2 T : TQ 2= PP 2: QQ 2. Так как P 2 P 1= 4 P 2 P , а 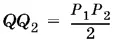, то QQ 2= 2 P 2 P . Поэтому P 2 T : TQ 2= 1 : 2, а значит, и PT : TQ = 1 : 2.

Ответ.B отношении 1 : 2.

1.52. Способ 1.Соединим точки P и T (рис. P.1.52, а ).

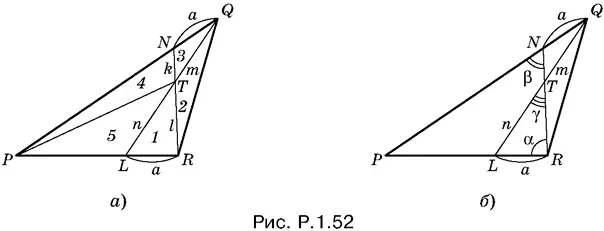
Пусть QN = RL = а , QT = m , TL = n , RT = l , TN = k . Обозначим треугольники, полученные из треугольника PQR : треугольник LTR — цифрой 1 , треугольник RTQ — цифрой 2 , треугольник QTN — цифрой 3 , треугольник NTP — цифрой 4 , треугольник PTL — цифрой 5 , а их площади или площади образовавшихся из них фигур буквой S с соответствующими индексами.

Треугольники 1 и 1 + 5 имеют общую высоту. Аналогично треугольники 3 и 4 . Поэтому

S 1 : S 1 + 5 = а : PR , S 3 : S 4 = а : PN ,

откуда

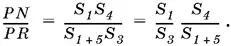
(7)

B треугольниках 1 и 3 углы при вершине T равны как вертикальные, т. е. S 1 : S 3 = ( nl ) : ( mk ). У треугольников 4 и 1 + 5 общая высота, соответствующая вершине P , т. е. S 4 : S 1 + 5 = k : l . Остается найти PN : PR из (7).

Способ 2.Пусть QN = RL = а , QT = m , TL = n (рис. P.1.52, б ). Обозначим угол NRP через α, угол PNR через β, а равные углы RTL и NTQ через γ.

Из треугольника PNR имеем

PN / PR = sin α/ sin β. (8)

Из треугольника NTQ имеем

a / m = sin γ/ sin β. (9)

Из треугольника LTR имеем

a / n = sin γ/ sin α. (10)

Разделим (10) на (9):

m / n = sin β/ sin α, т. е. в силу (8) PN / PR = n / m .

Ответ. n : т.

1.53.Так как ∠ MO 1 N = 60°, то MN сторона правильного вписанного в первую окружность шестиугольника. Ее длина равна радиусу первой окружности. На хорду MN (рис. P.1.53) опирается также вписанный в первую окружность ∠ MO 2 N , измеряемый половиной дуги MbN , которая равна 300°.

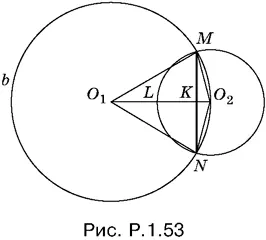
Поэтому центральный угол ∠ MO 2 N = 150°. Чтобы вычислить периметр фигуры MLNO 2, общей для обеих окружностей, нужно знать радиус второй окружности. Он равен длине любого из отрезков O 2 L , O 2 N и O 2М . Можно рассчитать из треугольника O 1 MO 2по теореме косинусов

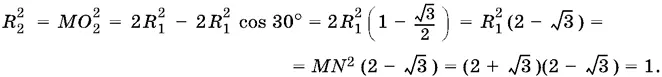
Теперь можно вычислить длины каждой из дуг MLN и MO 2 N: дуга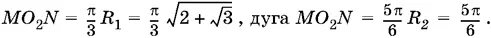

B сумме получим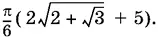

Ответ.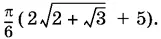

1.54.Пусть AB = а , BC = b , CD = с , DA = а , а опирающиеся на эти хорды углы равны соответственно α, β, γ, δ (рис. P.1.54).