Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

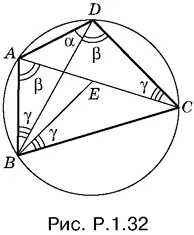
1.32. Способ 1.Пусть R — радиус окружности, а α, β и γ − вписанные углы, опирающиеся соответственно на стороны AB , BC и AD (рис. P.1.32). Углы, опирающиеся на одну и ту же дугу, равны (это отмечено на рисунке). Углы DBC и DAC тоже равны, и их нетрудно вычислить: ∠ DBC = ∠ DAC = π − (α + β + γ). По теореме синусов

AB = 2 R sin α, BC = 2 R sin β, DC = 2 R sin (α + β + γ), AD = 2 R sin γ.

Таким образом,

AB · DC + AD · BC = 4 R ² [sin α sin(α + β + γ) + sin β sin γ] = 2 R ² [cos(β + γ) − cos(2α + β + γ) + cos(β − γ) − cos(γ + β)] = 2 R ² [cos (β − γ) − cos(2α + β + γ)].

Так как

AC = 2 R sin (α + β), BD = 2 R sin (α + γ),

то

AC · BD = 4 R ² sin (α + β) sin (α + γ) = 2 R ² [cos (β − γ) − cos (2α + β + γ)].

Итак,

AB · DC + AD · BC = AC · BD .

Способ 2.Введем обозначения: AB = а , BC = b , CD = с , DA = d , AC = e , BD = f . Нужно доказать, что ac + bd = ef . Выберем на диагонали AC точку E так, чтобы угол CBE был равен γ. Тогда треугольники CBE и DBA подобны. Поэтому EC : b = d : f .

Из подобия треугольников ABE и DBC (углы ABE и DBC равны как равносоставленные) получаем AE : а = с : f . Определим из первого соотношения EC , а из второго AE и сложим эти два равенства:

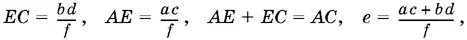
откуда ас + bd = ef , что и требовалось доказать.

1.33.Продолжим боковые стороны AB и CD трапеции (рис. P.1.33) до пересечения в точке S . Если через S и M (где M — середина BC ) провести прямую, то она пересечет AD в точке N , которая является серединой AD .

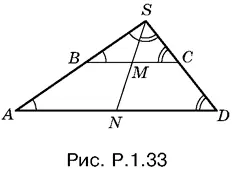
Из подобия треугольников BSM и ASN имеем

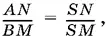
откуда

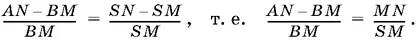
Так как по условию MN = AN − BM , то BM = SM и треугольник SMB равнобедренный. Аналогично доказывается, что треугольник SMC также равнобедренный. Следовательно, угол SMC равен удвоенному углу А , а угол SMB — удвоенному углу D (по свойству внешнего угла треугольника). Но оба этих угла SMB и SMC образуют развернутый угол. Следовательно, сумма углов А и D равна 90°.

1.34.Пусть AB = а , MR = x (рис. P.1.34).

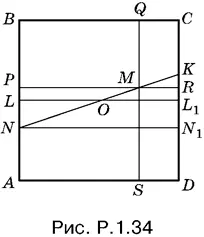
Выразим через а и x длины отрезков MQ , MS и MP . Ясно, что для этого достаточно найти длину отрезка QM , поскольку MS = а − QM , а MP = а − x . Так как QM = CR = CK + KR , то вычислим CK и KR . По условию AN = а / 3, а потому (треугольники OLN и OL 1 K равны) CK = а / 3. Чтобы найти KR , рассмотрим подобные треугольники MKR и NKN 1:

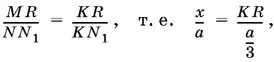
откуда KR = x / 3, а QM = а / 3+ x / 3. Остается убедиться в том, что числа а − x , 2 a − x / 3, а + x / 3, x образуют арифметическую прогрессию с разностью 2 x − a / 3.

1.35.Пусть CE = x (рис. P.1.35).

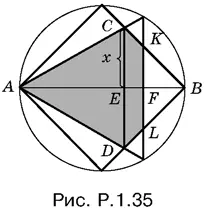
Выразим через x отрезок AE из треугольника ACE , в котором угол CAE равен 30°: AE = x √3 . С другой стороны, AE = AB − BE , а так как BE = CE = x , то AE = 2 − x . Итак, 2 − x = x √3 , откуда x = √3 − 1.

Заметим, что KF = FB = ½; площадь искомой фигуры равна

S ACD + S BCD − S BKL = 2 S ACB − S BKL .

Ответ.2√3 − 9/ 4.

1.36.Углы при нижнем основании трапеции и основании треугольника равны. Обозначим их через α. Тогда угол BAO равен углу ABO , т. е. равен 90° − α (рис. P.1.36). Поэтому угол OAD равен 2α − 90°. Так как треугольник MNO равнобедренный ( MO = NO ), то угол MNO равен α, а угол NOE равен 90° − (180° − 2α), т. е. равен 2α − 90°.

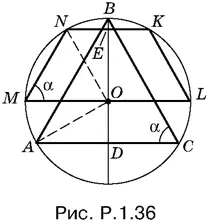
Треугольники ONE и AOD равны (по гипотенузе и острому углу). Следовательно, OE = AD . Кроме того, MO = OB , как два радиуса, и NE = OD , как стороны равных треугольников. Это означает, что BD = l .

По условию AD · BD = S , следовательно, OE = AD = S / l .

Ответ. S / l .

1.37.Из подобия треугольников AOD и BOC (рис. P.1.37) находим, что MO / NO = p , т. е. MN / NO = p + 1.

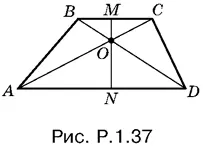
Отношение площадей трапеции и треугольника AOD можно записать в виде

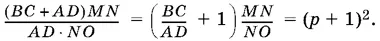
Ответ.( p + 1)².

1.38.Пусть R — радиус окружности, n — число сторон первого многоугольника, x — периметр третьего.

Периметры первого и второго многоугольников равны соответственно

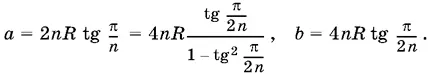
Периметр третьего равен

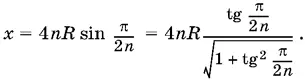
Сравнивая первые два выражения, найдем, что 1 − tg² π/ 2 n = b / a . Следовательно,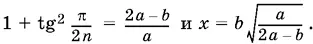

Ответ.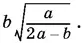

1.39.Если точки О и M расположены так, как показано на рис. Р.1.39, а , то NM > KL , так как хорда NM ближе к центру окружности. Но NM < а , а KL = 2 а . Получаем а < 2 а , что невозможно. Следовательно, фигуры расположены так, как показано на рис. Р.1.39, б .

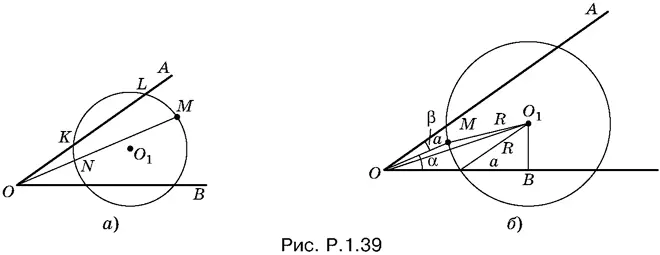
Центр рассматриваемой окружности лежит на биссектрисе угла AOB , так как точка О 1равноудалена от лучей AO и OB .