Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

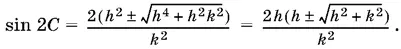
Если мы возьмем перед корнем знак минус, то получим sin 2 С < 0, чего быть не может, так как угол С острый, следовательно, 0 < 2 С < π.

Остается

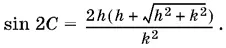
B правой части стоит положительное число. Чтобы можно было найти С , это число не должно превышать единицу, т. е.

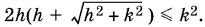
Неравенство можно переписать так:

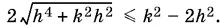
При возведении в квадрат необходимо добавить ограничение k ² − 2 h ² ≥ 0. Получим систему

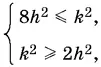
решением которой будет k ≥ 2√2 h , так как k и h по условию положительны.

Ответ.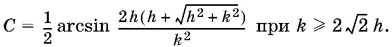

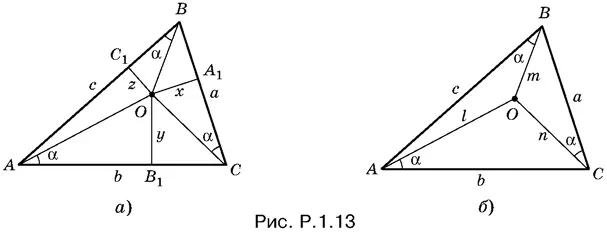
1.13. Способ 1.После того как из точки О опущены перпендикуляры длины x , y и z на стороны а , b и с соответственно (рис. P.1.13, а), можно записать

2 S = ax + by + cz .

С одной стороны, АО = y / sin α, а с другой стороны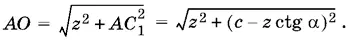

Таким образом,

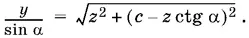
После простых преобразований получим

( y ² − z ²) cosec² α = c ² − 2 cz ctg α,

( x ² − y ²) cosec² α = b ² − 2 by ctg α,

( z ² − x ²) cosec² α = a ² − 2 ax ctg α,

где последние два уравнения выведены аналогично первому из рассмотренных отрезков CO и BO . Сложив все три уравнения, получим в левой части нуль, а в правой выражение, в которое входит S :

0 = ( a ² + b ² + c ²) − 2( ax + by + cz ) ctg α.

Таким образом,

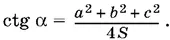
Способ 2.Так как площадь треугольника ABC равна сумме площадей трех треугольников, на которые треугольник ABC разбивается точкой O (рис. P.1.1З, б), то

S = ½ sin α ( an + bl + cm ).

Записав теорему косинусов для каждого из треугольников AOB , BOC , COA , получим

2 an cos α = a ² + n ² − m ²,

2 bl cos α = b ² + l ² − n ²,

2 cm cos α = c ² + m ² − l ².

Сложим три последних равенства:

2 cos α ( an + bl + cm ) = a ² + b ² + c ².

Используя полученное ранее выражение для S , исключим an + bl + cm .

Ответ.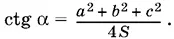

1.14.По условию CD = BC − AC (рис. P.1.14).

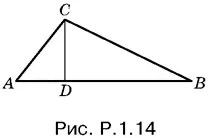
Так как

AC = CD / sin A , BC = CD / sin B ,

то

CD ( 1/ sin B − 1/ sin A ) = CD

или

sin А − sin B = sin A sin B .

Последнее уравнение можно переписать так:

4 sin A − B / 2cos A + B / 2 = cos ( А − B ) − cos ( А + B ).

Так как А − B = φ, то после замены

cos ( А + B ) = 2 cos² A + B / 2− 1

приходим к уравнению относительно y = cos A + B / 2:

y ² + 2 sin φ/ 2 y − cos² φ/ 2 = 0.

Из его корней

y 1, 2 = ±1 − sin φ/ 2

годится только первый, т. е.

cos A + B / 2 = 1 − sin φ/ 2.

Задача имеет решение при 0 < φ < π.

Остается решить систему

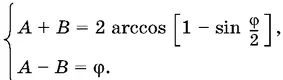
Ответ. А = arccos [1 − sin φ/ 2] + φ/ 2,

B = arccos [1 − sin φ/ 2] − φ/ 2

С = π − А − B .

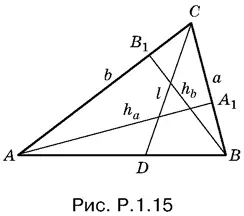
1.15.Площадь S треугольника ABC (рис. P.1.15) может быть записана с помощью биссектрисы l следующим образом:

S = ½( а + b ) l sin С / 2.

Теперь приравняем три выражения для 2 S :

аh а = bh b = ( а + b ) l sin С / 2.

Исключая а , получим

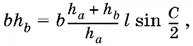
откуда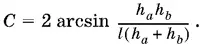

Задача имеет решение, если

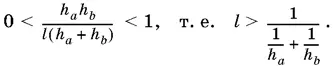
B правой части стоит величина, равная половине среднего гармонического длин h а и h b .

Ответ. 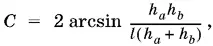если длина биссектрисы больше среднего гармонического длин h а и h b .

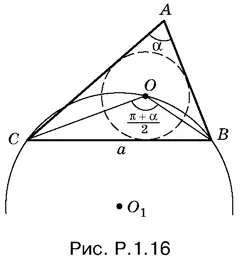
1.16.Так как ОС и OB (рис. P.1.16) — биссектрисы соответствующих углов треугольника ABC , то

∠ COB = π − (∠ OCB + ∠ OBC ) = π − B + C / 2.

Но B + С = π − А = π − α. Следовательно, ∠ COB = π/ 2+ α/ 2.

Применяя теорему синусов, получим

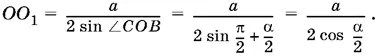
Ответ.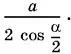

1.17. Проведем через центр О 1(рис. P.1.17) вписанной в треугольник ABC окружности прямую, параллельную AC и пересекающую медиану AE в точке О . Докажем, что О — точка пересечения медиан треугольника ABC .

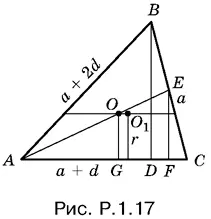
С помощью сравнения площадей получим ( а + d ) BD = rP , где

P = а + ( а + d ) + ( а + 2 d ) = 3( а + d ),

откуда BD = 3 r .

Так как AE — медиана, то из подобия треугольников BDC и EFC следует, что

EF = ½ D = 3/ 2 r .

Из подобия треугольников AOC и AEF получаем АО : AE = OG : EF = 2 : 3.