Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

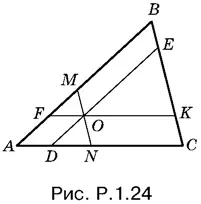
Поэтому

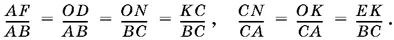
Следовательно,

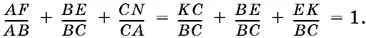
1.25.Обозначим угол AOD (рис. P.1.25) через α. Так как углы AOB и BOC равны 120°, то углы BOF и COE равны соответственно 60° − α и 60° + α. Составим сумму

AD ² + CE ² + BF ² = R ² sin² α + R ² sin² (60° + α) + R ² sin² (60° − α).

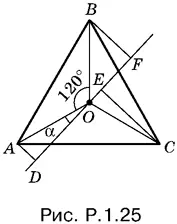
После понижения степени получим

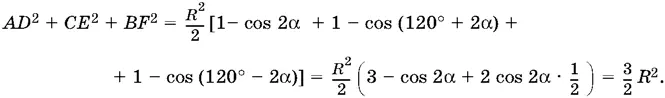
Тем самым доказано, что эта величина не зависит от положения прямой на плоскости.

1.26.По теореме косинусов

с ² = а ² + b ² − 2 ab cos С = 7,

откуда с = √7. По теореме синусов

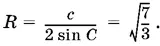
Угол AOB (рис. P.1.26) центральный, а угол ACB вписанный. У них общая дуга, следовательно, угол AOB равен 120°.

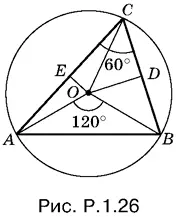
Применим теперь теорему синусов к треугольнику AOB :

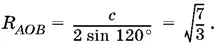
Оставшиеся величины R AOC и R BOC можно найти по формуле R = abc / 4 S .

Площади каждого из этих треугольников проще вычислить, если найти их высоты, опущенные из точки О :

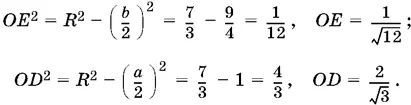
Таким образом, площади треугольников AOC и BOC равны 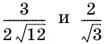соответственно, а радиусы окружностей, описанных около этих треугольников, равны 7/ √3и 7/ 4√3соответственно.

Ответ.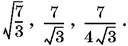

1.27.По теореме косинусов и в силу равенства а ² = с ( b + с ) получим b ² + с ² − 2 bc cos А = c ( b + с ), откуда

cos А = b − c / 2 c .

Данное в условии равенство можно записать так: с ² = а ² − bc , и сравнить его с теоремой косинусов для угла С . Получим

cos С = b + c / 2 a .

Нам нужно доказать, что угол А вдвое больше угла С . Вычислим для этого cos 2 С и сравним с cos А :

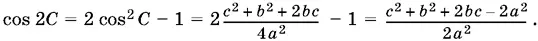
B выражение для cos А , которое мы получили раньше, сторона а не входит. Поэтому заменим в правой части полученной формулы а ² на bc + с ². Получим

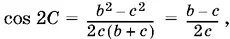
т. е. cos А = cos 2 С . Так как cos С = b + c / 2 a > 0, то угол С острый. Углы А и 2 С лежат между 0 и π, т. е. в интервале монотонности косинуса. Таким образом, из равенства косинусов следует равенство углов А = 2 С .

1.28.Центр О вписанный окружности лежит на пересечении биссектрис (рисунок сделайте самостоятельно). Поэтому

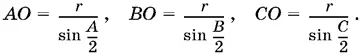
Подставляя в данное соотношение OA ² = OB · OC , получим

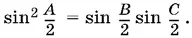
Применив к правой части формулу преобразования произведения синусов в сумму, приведем равенство к виду

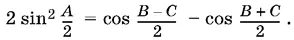
Заметив, что B + С = π − А , получим

cos B − C / 2= 2 sin² А / 2+ sin А / 2,

что и требовалось доказать.

1.29.По условию S = а ² − b ² − с ² + 2 bc . С другой стороны, S = ½ с sin А . Сравнивая эти выражения, получим а ² − b ² − с ² + 2 bc = ½ bc sin А .

Воспользуемся теоремой косинусов и заменим а ² на b ² + с ² − 2 bc cos А . После приведения подобных и сокращения на bc останется тригонометрическое уравнение

½ sin А = −2 cos А + 2,

которое можно переписать так:

sin А / 2cos А / 2= 4 sin² А / 2.

Так как А — угол треугольника, то А лежит в первой четверти и sin А / 2 ≠ 0. Наше уравнение принимает вид tg А / 2= ¼.

Ответ. А = 2arctg ¼.

1.30.Пусть О 1, О 2, О 3— центры квадратов, построенных на сторонах треугольника ABC (рис. P.1.30). Опустим из них перпендикуляры на стороны. Проведем средние линии DE и KE . На отрезках О 2 K и KE построим параллелограмм KELO 2.

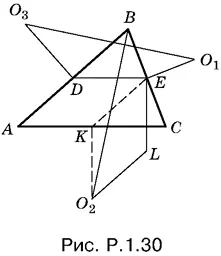
Рассмотрим четырехугольники О 1 EDO 3и BELO 2. При повороте около точки E одного из них на 90° он совпадает с другим (убедитесь в равенстве сторон и углов самостоятельно). Следовательно, отрезки О 1 О 3и ВО 2равны, что и требовалось доказать.

1.31.Достроим треугольник ABC до параллелограмма так, чтобы сторона AB была диагональю параллелограмма (рис. P.1.31).

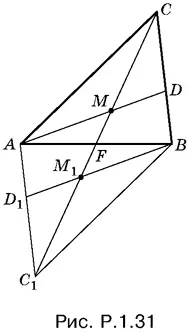
Проведем BD 1|| AD . Точку пересечения BD 1с диагональю CC 1параллелограмма обозначим через M 1. Треугольники MDC и M 1 BC подобны. Так как MF = CF / 4, то MC : MM 1= 3 : 2. Следовательно, MD : M 1 B = 3 : 5. Так как M 1 B = AM , то AM : MD = 5 : 3.

Площадь треугольника AFM в восемь раз меньше площади треугольника ABC , т. е. равна 8 . Высота треугольника AFM ( F — середина AB ), опущенная из вершины F , в два раза меньше высоты треугольника ABD , опущенной из вершины B . Так как AM : AD = 5 : 8, то площадь треугольника AFM относится к площади треугольника ABD как 5 относится к 2 · 8, т. е. как 5 : 16.

Зная, что площадь треугольника AFM равна ⅛, можно теперь найти и площадь треугольника ABD .

Ответ. 2/ 5.