Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

Следовательно, АО : ОЕ = 2 : 1 и О — точка пересечения медиан.

1.18.Площадь треугольника ABC (рис. P.1.18), с одной стороны, равна ½ h аа = 2 kr ², а с другой стороны, равна pr . Следовательно, p = 2 kr .

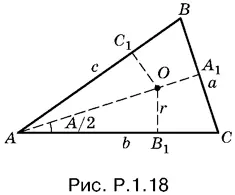
Так как АВ 1= АС 1(касательные к одной окружности) и аналогично BC 1= ВА 1, СВ 1= СА 1, то СВ 1+ BC 1= СА 1+ ВА 1= а , АВ 1+ СВ 1+ BC 1= p и АВ 1= p − а = 2 kr − kr = kr. Теперь можно вычислить

tg А / 2= r / kr = 1/ k .

Чтобы найти стороны b и с , определим величины b + с и bc . Величина b + с определяется просто:

b + с = 2 p − а = 3 kr .

Чтобы найти bc , вспомним, что площадь треугольника ABC , равная 2 kr ², может быть записана в виде ½ bc sin А , где sin А = 2 k / 1 + k ² (по формуле универсальной подстановки). Таким образом, bc = 2 r ²(1 + k ²).

Решая систему уравнений

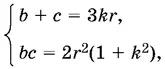
найдем

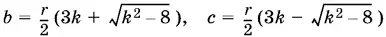
или наоборот

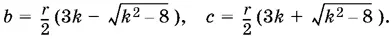
Задача имеет решение при k > 2√2.

Ответ.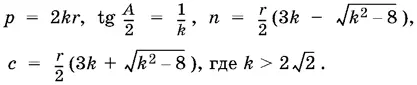

1.19.Так как углы С , А , B треугольника ABC образуют геометрическую прогрессию со знаменателем 2, то А = 2 С , B = 4 С (рис. P. 1.19). Точка О — центр вписанной окружности, т. е. OK и OL являются отрезками соответствующих биссектрис.

Вычислим углы треугольника OLK . Угол KOL равен углу BOA треугольника BOA , в котором два угла уже известны: угол при вершине А равен С , а угол при вершине B равен 2 С . Следовательно, угол BOA = π − 3 С . Но по условию π = А + B + С = 7 С , т. е. угол BOA , а следовательно, и угол LOK равны 4 С .

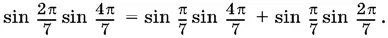
Рассмотрим далее треугольник EKC . Угол при вершине E в этом треугольнике (равный углу AEO из треугольника AEO ) вместе с углом OAE , равным С , образуют угол LOK , равный 4 С . Таким образом, угол KEC равен 3 С . Угол ECK равен половине угла ECM , который вместе с углом С образуют π, т. е. 7 С . Следовательно, угол ECK равен 3 С . Найденные два угла, каждый из которых равен 3 С , позволяют найти третий: угол OKL равен С .

Таким образом, подобие треугольников ABC и ОLK доказано.

1.20.Сумма всех углов треугольника равна 7 А . Поэтому

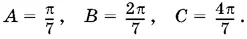
B силу теоремы синусов

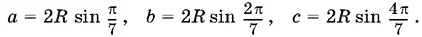
Соотношение, которое нужно доказать, эквивалентно такому:

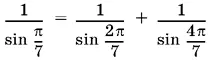
или

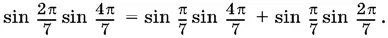
Преобразуем левую часть:

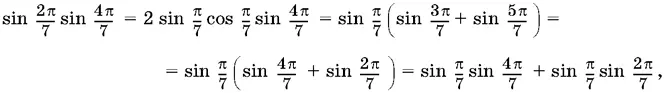
что и доказывает наше соотношение.

1.21.Проведем AL параллельно BC (рис. P.1.21).

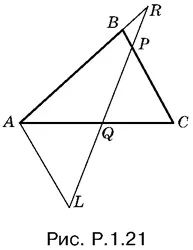
Из подобия треугольников RAL и RBP следует, что

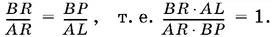
Из подобия треугольников AQL и CQP :

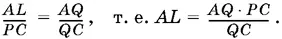
Подставляя значение AL в отношение, полученное раньше, придем к равенству

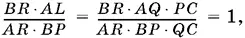
что и требовалось доказать.

1.22.Пусть AE — высота треугольника, опущенная на BC (рис. P.1.22). Тогда все участвующие в левой части равенства величины можно выразить через AE и длины отрезков, лежащих на BC . При этом следует стремиться связать каждый отрезок с точкой 1. Получим

AB ² = BE ² + AE ² = ( BD + DE )² + AE ².

AC ² = CE ² + AE ² = ( CD − DE ) 2+ AE ².

AD ² = DE ² + AE .

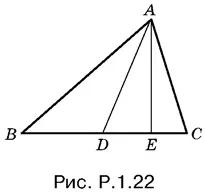
Воспользовавшись полученными соотношениями, составим сумму

AB ² · DC + AC ² · BD − AD ² · BC .

Раскрыв скобки и приведя подобные члены, получим

( DE ² + AE ²)( DC + BD − BC ) + DC · BD ² + BD · DC ².

Так как DC + BD = BC , то остается

DC · BD ² + BD · DC ² = ( BD + DC ) DC · BD = BC · DC · BD ,

что и требовалось доказать.

1.23.Проведем CE и AD параллельно BQ , а отрезки AP и CR продолжим до пересечения с ними (рис. P.1.23).

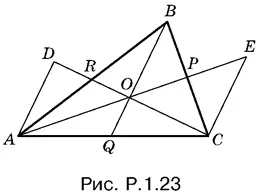
Рассмотрим образовавшиеся в результате подобные треугольники. Так как отрезки AD и OQ параллельны, то 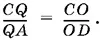Из подобия треугольников ADO и OEC следует, что 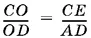. Итак, .

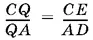Воспользовавшись двумя парами подобных треугольников: EPC и OBP , ADR и RBO , мы можем записать

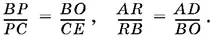
Следовательно,

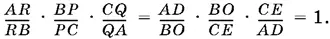
1.24.Треугольник ABC и три треугольника, образовавшихся внутри него (рис. P.1.24), подобны.