Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

1.1.Треугольник А 1 BC 1(рис. P.1.1) правильный, так как он подобен данному треугольнику ABC . Точки B , О , О 1и D лежат на одной прямой. Чтобы найти АО 1, нужно вычислить O 1 D . Но O 1 D = O 1 D 1− DD 1. Отрезок O 1 D 1равен трети отрезка ВD 1, как радиус окружности, вписанной в правильный треугольник А 1 BC 1. Таким образом, O 1 D 1= 2 R / 3. Отрезок DD 1мы найдем, если рассмотрим треугольник ABC , как вписанный в окружность с центром О :

DD 1= R / 2.

Отсюда O 1 D = 2 R / 3− R / 2= R / 6. Так как АD = ½ AC = R √3/ 2, то

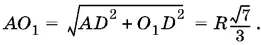
Ответ. R √7/ 3

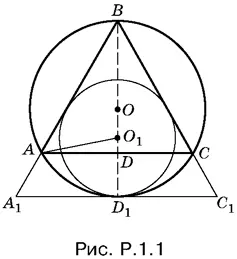
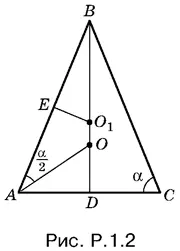
1.2.B треугольнике AOB (рис. P.1.2) известны: ∠ BAO = α/ 2, ∠ AOB = α/ 2+ π/ 2, BO = m · По теореме синусов находим AB = m ctg α/ 2· Теперь можно найти AC и R = ВО 1:

AC = 2 AD = 2 АВ sin ( π/ 2− α) = 2 АВ cos α = 2 m ctg α/ 2cos α,

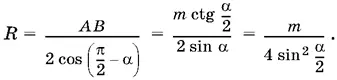
Ответ.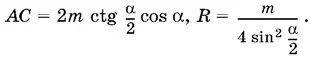

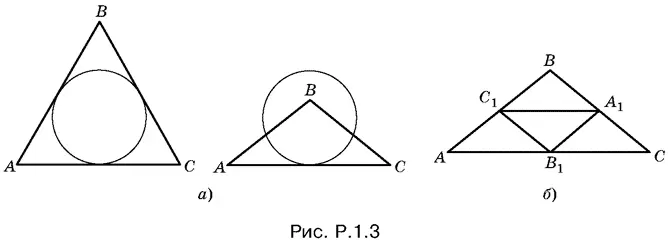
1.3.Условие задачи может быть геометрически осуществлено в двух случаях (рис. Р.1.3, а ), т. е. когда треугольник либо правильный, либо равнобедренный тупоугольный (докажите). Решить эту задачу можно сразу для обоих случаев. На рис. Р.1.3, б изображены треугольник ABC и треугольник А 1 В 1 С 1, составленные из средних линий первого треугольника. Треугольник А 1 В 1 С 1подобен треугольнику ABC с коэффициентом подобия половина. Следовательно, радиусы окружностей, описанных около этих треугольников, относятся как один к двум.

1.4.Если сторона а треугольника ABC биссектрисой АА 1разделена на отрезки а 1и а 2, то можно записать следующие соотношения (рис Р. 1.4.):

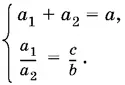
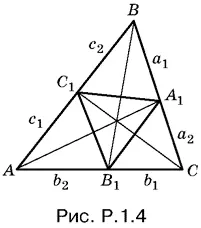
Решая эту систему уравнений относительно a 1и а 2, получим

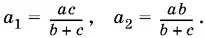
Вычислим аналогично отрезки, на которые разделены стороны b и с треугольника ABC :

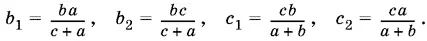
Так как отношение площадей треугольников, имеющих общий угол, равно отношению произведений сторон, между которыми лежит этот общий угол, то

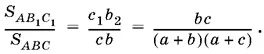
Аналогично находим

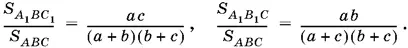
Теперь найдем отношение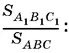

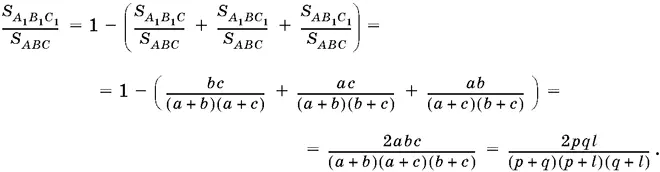
Ответ.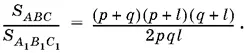

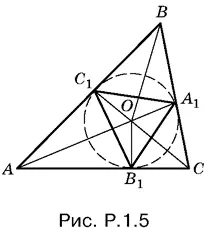
1.5.Выразим площадь треугольника ABC через радиус r вписанной окружности и углы А , B и С треугольника. Вначале запишем

S ABC = S AOB + S BOC + S COA

(рис. P.1.5).

Так как

S AOB = ½ АО · ВО sin OB ,

где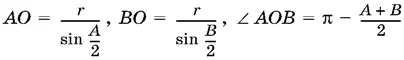

и, следовательно, sin ∠AOB = sin A + B / 2 = cos C / 2, то

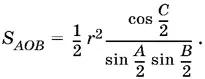
Аналогично находим S BOC и S COA и вычисляем искомую площадь:

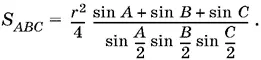
Выразим теперь через r , А , B и С площадь треугольника А 1 В 1 С 1. Разобьем и его на три треугольника:

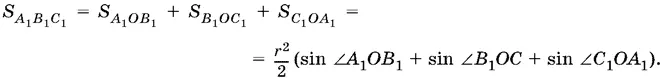
Чтобы найти угол А 1 ОВ 1, рассмотрим четырехугольник А 1 ОВ 1 С . B этом четырехугольнике два угла прямых, а потому два других — угол А 1 ОВ 1и угол С — образуют в сумме развернутый угол, т. е. угол А 1 ОВ 1равен π − С . Аналогично находим углы В 1 ОС 1и С 1 ОА 1.

Итак,

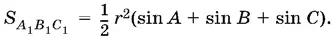
Остается найти отношение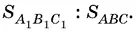

Ответ.2 sin A / 2 sin B / 2sin C / 2.

1.6.Так как B = 3 С , то из соотношения между площадями мы получим

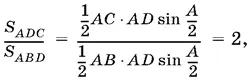
т. е. АС / AB = 2, откуда, в силу теоремы синусов, sin B / sin C = 2. Вспоминая, что по условию B = 3 С , придем к тригонометрическому уравнению sin 3 С = 2 sin С . Домножим обе части уравнения на cos С , получим sin 3 С cos 3 С = sin 2 С . Преобразовав левую часть в сумму синусов, придем к уравнению

sin 4 С + sin 2 С = 2 sin 2 С , или sin 4 С = sin 2 С .

Так как C — угол треугольника, меньший 1 (ведь 3 C и C — углы одного треугольника), то последнее уравнение может выполняться только в том случае, если

4 C = π − 2 C , т. е. C = π/ 6.

Находим остальные углы:

B = 3 С = π/ 2, A = π/ 3.

Ответ. π/ 3, π/ 6, π/ 2.

1.7.С одной стороны, площадь треугольника CAD (рис. Р.1.7) можно выразить через стороны b , l и угол между ними, а с другой стороны, — как сумму площадей треугольников АВС и ABD :