Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

18.16.Составить два уравнения относительно x и y нетрудно. Достаточно записать, чему равно время на путь от M до N и на путь от N до M , и вспомнить, что обе эти величины известны.

18.17.Данные в условии ограничения записать в виде системы неравенств и решить эту систему.

18.18.После того как заказчик выяснил, что выгоднее всего заказывать комплекты по 40 деталей, а наименее выгодны комплекты по 70 деталей, он должен позаботиться о том, чтобы общая сумма деталей равнялась 1100. При этом он будет стремиться заказать как можно больше дешевых комплектов и как можно меньше самых дорогих.

19.1.Свести задачу к сравнению ( n + 1/ n ) n и числа 2.

19.2.Нужно использовать условие, в силу которого а р , a q, а r и a s образуют геометрическую прогрессию. Это удобнее сделать так: a ² q = а ра r и т. п. (!!)

Остается выразить p − q , q − r и r − s через а р , a q , а r и a s и убедиться, что ( p − q )( r − s ) = ( q − r )².

19.3.При составлении разностей а − b , b − с и с − а удобнее пользоваться представлением чисел a , b и с с помощью арифметической прогрессии.

19.4.Воспользоваться тем, что log x b / a = log x с / b (числа a , b , с образуют геометрическую прогрессию).

19.5.Вынести за скобки 7/ 9.

19.6.Под знаком квадратного корня стоит полный квадрат 1/ 9(10 2 n − 2 · 10 n + 1).

19.7. После исключения получим уравнение относительно а1 и а 3, из которого следует, что а 1= а 3.

Так как а 1= а 3, то 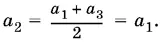Рассмотрите систему: а 1= а 2, а 2= а 3.

19.9.Теорема Виета, записанная для данного уравнения, приведет к системе уравнений относительно x 1и q (уравнение, в которое входит а , можно не рассматривать). Удобнее найти сначала q .

19.10.Записать произведение n первых членов и воспользоваться тем, что а 1= √2.

19.11.Если цифру сотен обозначить через а , а разность прогрессии — через d , то число делится на 5, когда либо а + 2 d = 0, либо а + 2 d = 5; оно же делится на 9, если а + ( а + d ) + ( а + 2 d ) делится на 9. Остается воспользоваться тем, что а , а + d и а + 2 d — цифры.

19.13.B задаче спрашивается, сколько комбайнов было в колхозе. Эту величину мы обозначим через n . Условия задачи позволяют составить три уравнения. При этом левая часть уравнения, соответствующего работе по плану, представляет собой сумму членов арифметической прогрессии. (!!)

При решении системы уравнений нужно исключить x и y .

19.14.При решении уравнений нужно иметь в виду, что нас интересуют только а и q .

19.15.Двух уравнений достаточно для решения задачи, так как нас интересуют не сами числа а , b и с , а отношение каких-либо двух из них. Поскольку полученные результаты использования условий задачи уравнения однородны относительно а , b и с , то определить интересующую нас величину нетрудно.

19.16.Так как предел (¼) n при n → ∞ равен нулю, то а n и b n имеют общий предел.

19.17.Члены двух арифметических прогрессий, имеющих первый член, равный нулю, могут снова образовать арифметическую прогрессию в том и только в том случае, если разность одной прогрессии кратна разности другой прогрессии.

20.1.Воспользоваться оценкой

1/ (1 + k )²< 1/ (1 + k ) k .

20.2.Воспользоваться тем, что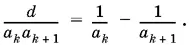

20.4.Умножить правую часть на а − 1 и привести ее к виду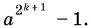

20.5.Разбить полученную сумму на три алгебраических слагаемых: 2 n , произведение n на сумму чисел от 1 до n − 1 и сумму квадратов этих же чисел.

20.6.Бесконечная геометрическая прогрессия имеет сумму, если она бесконечно убывающая, т. е. |2 x | < 1.

20.8.Рассмотреть разность S n − S nx ², в которой выделить геометрическую прогрессию.

20.9.Полученные равенства сложить и воспользоваться известными формулами для S n , S n ², S n ³.

20.10.Подсчитайте число четных (нечетных) членов, стоящих до n -й группы.

20.11.Каждое слагаемое после домножения на 2 sin π/ 2 n представить в виде разности косинусов.

20.12.Нетрудно заметить, что ряд 2 S отличается от ряда S на величину, которая легко может быть сосчитана.

20.13.Запишем два соседних члена ряда: 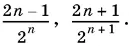Если первый член разделить на 2 и вычесть из второго, получим 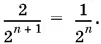Это должно подсказать соответствующую процедуру с рядами. Только не забудьте предварительно обозначить искомую сумму через S .

21.1.Так как сосед справа и сосед слева неразличимы, то можно любого из сидящих оставить на месте, а остальных попросить пересесть на место, симметричное относительно того, кто остался на своем месте.

21.2.Обратить внимание на то, что, вычитая перестановки, в которых на первом месте стоит элемент а 1, и перестановки, в которых на втором месте стоит элемент а 2, мы некоторые перестановки вычтем дважды.

21.3.Поскольку в нашем распоряжении имеются семь разрядов, то выбрать места для трех двоек можно 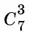способами.

21.4.Число не может начинаться с цифры 0. На сколько больше чисел мы получим, если не учтем это обстоятельство?

21.5.Экскурсантов для заселения первой каюты можно выбрать 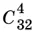способами, вторую каюту нужно заселить четырьмя из оставшихся и т. д.

21.6.Доказать, что .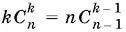

21.7.После упрощений мы придем к квадратному уравнению относительно n и k , которое нужно решить в целых числах. Удобнее решать это уравнение относительно k .