Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы
- Название:Сборник задач по математике с решениями для поступающих в вузы
- Автор:
- Жанр:
- Издательство:«ОНИКС 21 век» «Мир и Образование»
- Год:2003
- Город:Москва
- ISBN:5-329-00766-6, 5-94666-080-2
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы краткое содержание
Основу задачника составили варианты письменных работ по математике, предлагавшихся на вступительных экзаменах в ряде ведущих вузов Москвы.
Сборник содержит около 500 типовых задач. K каждой задаче дается до трех указаний, помогающих найти правильный путь к решению, а затем приводится подробное решение.
Пособие может использоваться при самостоятельной подготовке к экзаменам в вуз, а также на подготовительных отделениях и курсах.
Сборник задач по математике с решениями для поступающих в вузы - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
14.12.Произведение cos x cos 3 x , стоящее в знаменателе, выразить через cos 2 x . Получится алгебраическое неравенство относительно y = cos 2 x .
14.13.При возведении неравенства в квадрат достаточно потребовать, чтобы cos x ≥ 0.
14.15.Обозначить sin α через y и разложить получившийся многочлен третьей степени на множители, воспользовавшись теоремой о делителях свободного члена и первого коэффициента.
14.16.Выражение 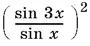 можно преобразовать, воспользовавшись разложением sin 3 x = sin (2 x + x ).
можно преобразовать, воспользовавшись разложением sin 3 x = sin (2 x + x ).
14.17.Так как абсцисса вершины параболы оказывается внутри интервала −1 < z < 1, а сама парабола направлена рогами вверх, то условие задачи равносильно тому, что ордината вершины положительна.
К главе 15
15.1.Неравенство сводится к квадратному, если положить log sin x 2 = y . При этом необходимо следить за равносильностью преобразований.
15.3.Поскольку основание логарифма больше единицы, неравенство между логарифмами можно заменить таким же неравенством между cos x и tg x .
15.4.Остается перейти к системе тригонометрических неравенств, равносильной логарифмическому неравенству. При этом нужно помнить, что все функции, стоявшие в условии под знаками логарифма, должны быть положительными.
15.5.Для дальнейшего нужно иметь в виду, что условие 0 < | а | < 1 не равносильно неравенству −1 < а < 1.
15.6.При дальнейшем решении мы столкнемся с выбором целочисленного аргумента. Следует помнить, что мы имеем дело с |lg x |, а не с lg x .
15.7.Неравенство равносильно условию, что знаменатель положителен, если при этом arccos ( x ² − 3 x + 2) существует и отличен от нуля.
15.8.Если 1 − x > 0, то правая и левая части неравенства попадают в интервал от 0 до π/ 2, который является общим интервалом монотонности для тангенса и косинуса. Если взять косинус от правой и левой частей неравенства, а знак неравенства изменить на противоположный, то получим неравенство, равносильное данному.
15.9.Неравенство 4 x − x ² − 3 > 1 удовлетворяется лишь при x = 2. Докажите, что тогда оба сомножителя должны быть раны единице.
15.10.Первая система не имеет решения, поскольку из условия А = 0 следует, что tg x = 1. Но tg x стоит в основании логарифма и не может быть равным единице. Остается решить вторую систему, которую можно упростить, заметив, что tg x > 1.
К главе 16
16.3.При исследовании нужно помнить, что отрицательное число в дробной степени не имеет для нас смысла.
16.4.Решив простейшее тригонометрическое уравнение, получим показательное уравнение, которое нужно исследовать, в зависимости от значений, принимаемых целочисленным аргументом.
16.5.Вспомнить, когда произведение синусов и косинусов может равняться единице.
16.7.Полученное уравнение легко решить, если записать sin³ x = = sin x (1 − cos² x ). При решении распадающегося уравнения, которое получится в результате такой замены, нужно постоянно иметь в виду ограничения.
16.8. При решении удобно на время забыть о возникающих ограничениях, а в конце проверить, для каких из найденных значений неизвестного они выполняются.
16.9.Использовать тот факт, что x > 0.
16.10.При исследовании полезно иметь в виду, что cos x ≤ 1 и дискриминант квадратного уравнения не должен быть отрицательным.
16.11.Удобно отдельно рассмотреть случаи а ≤ −1, а ≥ −1, когда данное уравнение имеет неотрицательный дискриминант.
16.12.Вы должны получить систему, состоящую из двух уравнений, трех неравенств и двух ограничений ≠.
16.13.Обозначив 4 cos² π x через u ( u > 0), найдем, что левая часть, равная 4/ u + u , не может стать меньше 4. Чтобы оценить квадратный трехчлен, стоящий в правой части, можно выделить полный квадрат.
16.14. 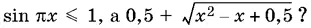
К главе 17
17.1.Осуществить замену переменных: x − 1 = y , 2 x + 1 = z . Найти f ( y ) и g ( z ), что равносильно знанию f ( x ) и g ( x ).
17.2.Уравнение f ( f ( x )) = 0 имеет корни x 1= 0 и x 2= 3. Исследование функции y = x ³ − 6 x ² + 9 x − 3 позволит определить число оставшихся корней интересующего нас уравнения.
17.3.Первое уравнение после подстановки примет вид
5 · 2 x ² − 2 xy + 1= (1 + 2 k )3 y ² − 1,
k — целое. При каких y в правой части не будет множителя 3?
17.4.Полученное после подстановки квадратное уравнение относительно z имеет дискриминант, равный (3 y − 1/ y )² , что позволяет непосредственно рассмотреть возможные корни.
17.5.Касание функций f ( x ) и F ( x ) в точке М 0( x 0; y 0) означает совпадение ординат f ( x 0) и F ( x 0), а также угловых коэффициентов касательных при x = x 0, т. е. значений f′ ( x 0) и f ( x 0).
17.6.Будьте внимательны в отношении точек границы множества решений и определите, какие из них принадлежат этому множеству, а какие не принадлежат.
17.7.Прямая y = − x позволит отсечь от части плоскости, координаты точек которой удовлетворяют первому неравенству — фигуру, площадь которой нас интересует.
17.8.Прямые AC и BD пересекаются в точке E (4; 4). Прямая BC параллельна оси абсцисс и пересекает ось ординат в точке G . Через точку D проведем прямую DF , параллельную оси абсцисс и пересекающую ось ординат в точке F , а прямую AC — в точке H . Пусть CK — перпендикуляр, опущенный из точки С на FD . Теперь искомую площадь легко найти через площадь прямоугольника FGCK и прямоугольных треугольников, которые будут изображены на рисунке после всех проведенных выше построений.
17.9.После замены переменных и простых преобразований исходные неравенства примут вид
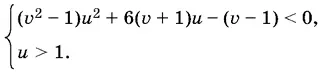
Проекция множества решений этой системы рассматривается на прямую u = 2. Левую часть первого из неравенств рассмотрите как функцию второго порядка относительно u , где зависящие от v коэффициенты — параметры. Тогда можно сформулировать условия существования решений в зависимости от значений v . (Куда направлены ветви параболы и каков знак дискриминанта.) (!!)
Читать дальшеИнтервал:
Закладка:










