Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

10.41.Разобрать случаи, позволяющие раскрыть знаки абсолютных величин. Таких случаев будет четыре.

10.42.Так как x − 2 > 0, то x − 1 > 1 и, следовательно, ( x − 1)² > 1.

10.43.Из условия, что log 2(2 − 2 х ²) > 0, легко вывести, что |√2 | x |- 1| ≤ 1.

10.44.Перейти от неравенств между функциями к неравенству между аргументами и учесть необходимые ограничения.

10.46.Для положительного основания (обозначим его f ( x )) нужно решить две системы

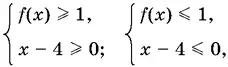
которые равносильны неравенству

( f ( x ) − 1)( x − 4) ≥ 0.

При f ( x ) < 0 следует рассмотреть случаи, когда показатель степени x − 4 — четное число.

10.47.Известно, что при неположительном дискриминанте знак квадратного трехчлена не может быть противоположен знаку старшего коэффициента. Если же дискриминант положителен, то такие точки всегда найдутся.

10.48.Поскольку из ложного утверждения следует все, что угодно, решение распадается на две части: а) находим значения а , при которых первое неравенство не имеет решений, тогда из него следует второе; б) если первое неравенство имеет решения, то они не должны выйти за рамки решений второго неравенства.

10.49.Рассмотрите варианты расположения параметра а относительно интервала (1, 2). Особое внимание обратите на граничные точки этого интервала.

10.50.Неравенство

( x + 5)[( x + 3) · 2 2 + x − (2 + x )] > 0

при x = −5 не удовлетворяется. Остается рассмотреть случаи x + 5 < 0 и x + 5 > 0. Далее удобно рассмотреть и случаи x + 3 < 0 и x + 3 > 0 ( x + 3 = 0 тоже не является решением неравенства). (!!)

Решить неравенства

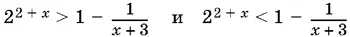
удобнее, изобразив графически функции, стоящие в левой и правой частях этих неравенств.

10.52.Данное неравенство можно преобразовать к виду:

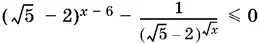
или

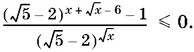
10.53.Левую часть неравенства следует преобразовать к виду

1 − | у |².

11.1.Остается заметить, что lg 2 + lg 5 = 1.

11.3.Привести уравнение к равенству степеней с одинаковыми показателями.

11.4.Обратить внимание на тот факт, что поскольку у = 3 −| x − 2|, то 0 < у ≤ 1.

11.7.Если обе части уравнения разделить на 2 + √3, то придем к квадратному уравнению относительно у = (2 + √3) x ² − 2 x .

11.8.Совсем нетрудно найти один корень уравнения. Затем нужно попытаться доказать, что других решений нет. (!!)

Корнем будет x = 2. Докажите, что других корней нет, используя монотонность показательной функции.

11.10.Левую часть выразить через у = log 3(3 x − 1).

11.11.Можно обозначить log x 7 = у , но удобнее использовать другое обозначение. Какое — станет ясно, если дополнить правую часть до полного квадрата (суммы или разности?).

11.14.Когда мы заменим log x 4 · log 4 x единицей, получим уравнение, которое может иметь посторонний корень x = 1. Поскольку в дальнейшем нам придется потенцировать, что снова может повлечь приобретение посторонних корней, решение необходимо закончить проверкой.

11.15.При переходе к логарифмам с основанием x мы можем потерять корень. Какой?

11.16.Чтобы воспользоваться формулой модуля перехода, нужно умножить обе части уравнения на log 2(3 + x ).

11.17.Если умножить уравнение на выражение, стоящее в знаменателе, то нужно потребовать, чтобы последнее не обращалось в нуль, т. е. | x ² + x − 1| ≠ 1. При потенцировании же появится еще одно ограничение.

11.18.Теперь с помощью тождества, эквивалентного определению логарифма, данное уравнение можно свести к квадратному относительно x log ba .

11.19.Нужно помнить, что √ c ² = | с |, и разобрать несколько случаев, предварительно оценив из условия log а x и а . Для оценки а удобно воспользоваться неравенством t + 1/ t ≥ 2 при t > 0.

11.20.Первое из уравнений, полученных после логарифмирования, разделить на второе и затем произвести потенцирование.

11.21.Нужно заметить, что 243 = 3 5, 1024 = 2 10. Теперь из второго уравнения системы с помощью первого нетрудно получить уравнение относительно (⅔) y .

11.22.Для того чтобы найти 4√ x + √ у , можно второе уравнение возвести в степень 3/ 2и полученное выражение использовать для подстановки в первое уравнение системы.

11.23.Выразить 11 xz , 11 z и 11 ( x − 1) z через 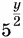и подставить в тождество, записанное в первом указании (см. с. 146).

11.24.Если в левой части второго уравнения вынести за скобки 2 x + 2 у , то в скобках останется выражение, аналогичное левой части первого уравнения. Его можно заменить числом 2.

11.25.Здесь удобно не заботиться о равносильности, а каждый раз получать следствия. Алгебраическая система, которая будет получена, легко сводится к уравнению относительно u = у / x . Для этого нужно будет почленно перемножить входящие в нее уравнения.

11.26.При преобразовании выражений, входящих в первое уравнение (после подстановки), нужно будет воспользоваться определением логарифма.

11.27.Так как xy = 3, то либо x , либо у больше единицы. Мы убедились, что x и у положительны. Следовательно,

x + y > 1 и |log 2( x + у )| = log 2( x + у ).

Остается рассмотреть два случая в зависимости от знака log 2( x − у ).

11.29.Воспользоваться математической записью определения логарифма: а log ab = b .

11.30.Определив x , следует использовать его для упрощения третьего уравнения системы. Если третье уравнение преобразовать в алгебраическое, то посмотрите, что при этом может произойти — потеря или приобретение корней.

12.2.Доказательство следует начать с очевидного тождества

tg [(30° − α) + (60° − α)] = ctg 2α.

12.3. Воспользоваться тем, что

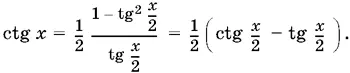
12.6.Вычислить произведение синусов несколько труднее. Удобнее найти квадрат этого произведения, записав 2 sin 2 π/ 7как 1 − cos 2π/ 7и т. д.