Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

9.35.Все прямые у = а ( x + 5) + 4 проходят через точку (−5; 4). Построение графика функции у = |6 − | x − 3| − | x + 1|| удобно начать с построения графика функции

у = 6 − | x − 3| − | x + 1|.

9.36.Уравнение равносильно системе

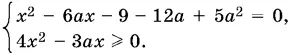
У первого уравнения есть корни

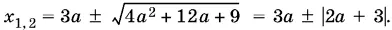
Остается выяснить, когда их два, а когда один, а также, при каких а для каждого из них удовлетворяется участвующее в системе неравенство.

9.37.Для упрощения симметрических многочленов применяют подстановку x + 1/ x = t . Здесь возможна похожая подстановка. Наличие в числителе каждой дроби множителя x упрощает решение.

9.38.Вы упростите вычисления, если обратите внимание, что 84 693 делится на 327.

10.1.Ввести обозначения а = 1 + k и b = 1 − k .

10.2.Обозначим выражение, стоящее в левой части неравенства, через P . Разделив его на а 1 а 2 ...а n = 1, после несложных преобразований получим

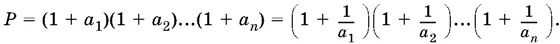
Для оценки P удобно рассмотреть теперь Р ² и заметить, что

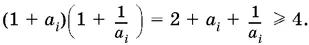
10.3. Способ 1.Воспользоваться тем, что с > а и с > b , и оценить каждое слагаемое.

Способ 2.Применить свойство показательной функции, приняв во внимание, что а < с , b < с .

10.5.Использовать условие а + b + с = 1, чтобы убедиться, что неравенство будет обязательно строгим.

10.7.Показательная функция ( a / b ) x , в силу условия задачи, является возрастающей.

10.8.Применить неравенство между средним арифметическим и средним геометрическим к произведению каждых двух чисел, равноотстоящих от концов в выражении n !.

10.9. Способ 1.В неравенстве (1 − u )( v − 1) > 0 (см. указание I на с. 141) раскрыть скобки и воспользоваться неравенством между средним арифметическим и средним геометрическим чисел uv и w .

Способ 2.Воспользоваться неравенством u / v + v / u > 2 (сложить его с полученным в указании I).

10.10.Оценить произведение ( p − а )( p − b )( p − с ) суммой этих чисел можно, воспользовавшись неравенством

xyz ≤ (x + y + z)³/ 27.

10.12.Зная выражения у + z и уz через x , можно записать квадратное уравнение с коэффициентами, зависящими от x , корнями которого будут у и z .

10.13.Выразив у + z и уz через x , придем к квадратному уравнению, коэффициенты которого зависят от x . Поскольку в условии сказано, что x , у и z — действительные числа, дискриминант полученного уравнения не должен быть отрицательным. (!!)

Найденные границы изменения x , в силу симметрии данных уравнений, распространяются на у и z .

10.15.Чтобы данный трехчлен был отрицательным внутри некоторого отрезка, необходимо и достаточно, чтобы на концах отрезка он принимал неположительные значения.

10.16.Доказать, что условие а > 0 несовместно с требованием, в силу которого оба корня больше а .

10.17.Так как k ≠ 0 (иначе условие задачи неосуществимо), то парабола должна иметь один корень в интервале (−1, +1), а другой вне этого интервала.

Такое расположение параболы имеет место тогда и только тогда, когда значения трехчлена в точках −1 и 1 противоположны по знаку.

10.18.Если ветви параболы будут направлены вверх и, кроме того, парабола не будет пересекать положительную полуось Оx , то мы получим расположение параболы, необходимое и достаточное для выполнения условия задачи.

10.22.Числитель и знаменатель полученной дроби должны иметь разные знаки. Приходим к совокупности двух систем.

10.23.Неотрицательный множитель можно отбросить, исключив точки, в которых он обращается в нуль. Оставшееся неравенство удобно привести к виду, в котором правая и левая части неотрицательны, и возвести в квадрат с учетом соответствующих ограничений.

10.24.При x > 0 данное неравенство можно возвести в квадрат (учтя соответствующие ограничения), так как обе его части положительны. При x < 0 неравенство исследуется аналогично.

10.25.Составить квадратное неравенство относительно

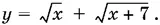
10.26.Нельзя забывать о том, что под корнем должно стоять неотрицательное число, в то время как само а может быть и отрицательным.

10.27.Данное неравенство можно переписать в виде

2 2 x ≤ 3 · 2 √ x · 2 x + 4 · 2 2√ x .

Поделив на 2 √ x · 2 x , получим неравенство, сводящееся к квадратному.

10.29.При x < 0 неравенство может удовлетворяться лишь при условии, что 2 x − 1/ 3 − x = n — целое. Отберите те значения n , при которых число x оказывается отрицательным, и ответьте на вопрос, что будет при x = 0.

10.30.Выражение х ³ − 5 х + 2 легко разложить на множители методом группировки: ( х ³ − 4 х ) − ( x − 2).

10.31.Нужно рассмотреть два случая в зависимости от расположения а относительно единицы.

10.32.Случай x = 0 исследуется непосредственной подстановкой. При x < 0 показатель степени должен быть целым числом. Здесь придется рассмотреть подслучаи в зависимости от того, будет ли это целое число четным или нечетным.

10.35.Если после приведения всех логарифмов к общему основанию перенести все члены неравенства в одну часть, то полученное выражение разлагается на множители, одним из которых будет 2 log 5 x + 1.

10.36.Обозначив log 2(2 х − 1) = y , можно привести это неравенство к квадратному.

10.38.После решения алгебраического неравенства нужно вернуться к прежним обозначениям. При этом приходится рассмотреть различные случаи в зависимости от величины а .

10.39.Обозначить log kx через y , после чего получится неравенство относительно y , которое решается методом интервалов.

10.40.Так как под знаком логарифма стоит число 4 х − 6, то x не может быть меньше единицы.