Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

12.7.Разделить числитель и знаменатель выражения, стоящего в правой части, на Вb .

12.8.Если заменить sin² x на k ² sin² у , то sin² у можно вынести за скобки.

12.9.Выразить а ² + b 2через cos α − β/ 2.

12.10.Обозначить sin²α = а , sin²β = b , sin²γ = с и преобразовать данное равенство, выполнив сложение.

12.11.Привести к общему знаменателю и все произведения тригонометрических функций от α + π/ 3и α + 2π/ 3преобразовать в сумму.

12.13.Второе слагаемое преобразуется к выражению −2 cos² 8° или cos 16° − 1.

13.1.Заменить √2 sin ( x + π/ 4) на sin x + cos x , после чего объединить все одночлены, содержащие cos З x , и все оставшиеся одночлены уравнения. Это поможет получить распадающееся уравнение, y которого в правой части нуль, а левая разложена на множители.

13.2.Если левую часть представить в виде 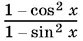, то получим распадающееся уравнение, которое нужно решать, следя за равносильностью.

13.3.Левую часть уравнения записать в виде 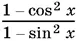, перенести все в одну часть и вынести 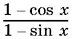за скобки. (!!)

Оставшееся в скобках выражение симметрично относительно sin x и cos x . Если привести дроби к общему знаменателю, то должно получиться достаточно простое выражение, поскольку все подобные члены будут иметь разные знаки.

13.4.Найти такие решения уравнения sin 2 x sin 7 x = cos 2 x cos 7 x , при которых cos 2 x cos 7 x ≠ 0.

13.5.Замена ctg x = 1/ tg x приведет к появлению tg x множителем в числителе. Однако tg x не может быть равным нулю.

13.6.Воспользоваться формулой разности тангенсов и заменить полученное уравнение эквивалентной ему системой, состоящей из нового уравнения и ограничений.

13.7.Множитель sin ( x + π/ 4) входит в правую часть уравнения. Чтобы обнаружить это, достаточно заменить cos x на sin ( π/ 2 − x ) и привести правую часть к виду, удобному для логарифмирования.

13.8.После приведения к виду, удобному для логарифмирования, внимательно следить за равносильностью.

13.9.Так как cos x / 2на интервале 0 < x / 2< π меняет знак, то этот интервал придется разбить на два: 0 < x / 2 ≤ π/ 2, π/ 2< x / 2< π.

13.10.При решении получившегося уравнения нужно правильно оценить роль параметра: если из соотношения исчезает неизвестное и остается только параметр, то при данном значении параметра неизвестное может принимать любое значение из области определения данного уравнения.

13.11.Выбор значений x , попадающих в интервал 0 ≤ x ≤ 2π, удобнее осуществить, если при решении мы постараемся воспользоваться арккосинусами, областью значений которых является указанный интервал.

13.12.Под радикалом стоит полный квадрат. Помните, что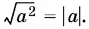

13.13.Остается заметить, что tg x + sin x = tg x (1 + cos x ), а tg x − sin x = tg x (1 − cos x ). Оба этих выражения входят слагаемыми в степени ½. Множитель tg ½ x входит и в третье слагаемое. Этот множитель можно вынести за скобки, так как 1 + cos x и 1 − cos x никогда не станут отрицательными, а следовательно, равносильность в результате этого действия не нарушится. (!!)

Получаем уравнение вида tg ½ x φ( x ) = 0, где φ( x ) имеет смысл всегда. Это уравнение равносильно совокупности уравнения tg x = 0 и системы

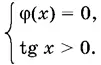
(B ограничении взято строгое неравенство, так ка случай tg x = 0 учтен раньше.)

13.14.Чтобы произвести упрощения, придется воспользоваться еще одним условным тождеством 1/ tg 2 x = ctg 2 x . Провести анализ равносильности и перейти в полученном уравнении к синусам и косинусам.

13.15.Когда в уравнение входят только sin α cos α и sin α + cos α, то одну из этих величин, например вторую, можно обозначить через y , а другую выразить через y .

13.16.Перейти к функциям x и привести уравнение к однородному, домножив 6 sin x на тригонометрическую единицу.

13.17.Воспользоваться теоремой о рациональных корнях многочлена с целыми коэффициентами.

13.18.Выразить правую и левую части через y = cos x / 2.

13.19.Выражение в квадратных скобках представить в виде

(1 + ctg x ) + [ 1 + ctg ( π/ 4 − x ) ]

и воспользоваться формулой суммы котангенсов. B правой части для cos 2 x нужно выбрать выражение, которое позволит избавиться от стоящей в скобках единицы.

13.21.Относительно cos x получится биквадратное уравнение, решения которого придется исследовать.

13.24.Воспользоваться этой формулой еще раз, предварительно выделив выражение 1 + cos 2 x , и получить распадающееся уравнение. (!!)

Вспомнить об условиях, при которых произведение двух косинусов равно единице.

13.25.Записывая условие одновременного равенства двух косинусов единице или минус единице, следует брать разные обозначения для целочисленного переменного.

13.26.Если перенести все в правую часть, то мы сможем образовать сумму двух неотрицательных слагаемых.

13.27.Так как cos 3 x ≥ 0, а при дополнении до полного квадрата к обеим частям уравнения прибавляется ± cos x cos 3 x , то знак правой части зависит от знака cos x . Это означает, что целесообразно рассмотреть три случая: cos x = 0, cos x > 0, cos x < 0. (!!)

Если cos x > 0, то целесообразно привести левую часть к квадрату разности, а если cos x < 0 — к квадрату суммы.

13.28.Поскольку минимум левой части совпадает с максимумом правой, то единственная возможность их уравнять — решить систему

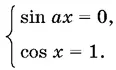
13.29.При решении окажется полезной следующая идея. Если уравнение преобразуется к виду f ( x ) g ( x ) = 0, причем корни f ( x ) находятся легко и содержат все корни g ( x ), то решать уравнение g ( x ) не следует. Поскольку в нашем случае уравнение f ( x ) g ( x ) = 0 было получено из системы, то остается выяснить, какие из корней уравнения f ( x ) = 0 приведут к решению исходной системы.