Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

8.13.Записать x 4+ 1 в виде произведения квадратных трехчленов с неопределенными коэффициентами, раскрыть скобки и воспользоваться условием равенства двух многочленов.

8.14.Многочлен делится на у ³, если его свободный член и коэффициенты при у и у ² равны нулю.

8.15.Воспользоваться условием тождественного равенства двух многочленов.

9.3.Один способ — дополнить левую часть до полного квадрата, второй — обозначить второе слагаемое через u ² и перейти к системе.

9.4.При возведении в куб воспользоваться формулой куба суммы в виде ( а + b )³ = а ³ + b ³ + 3 аb ( а + b ). Выражение а + b заменить правой частью данного уравнения.

9.6.Если ввести новое неизвестное p = u + v , то с помощью уравнения u − v = 1 можно через p выразить как u , так и v . Это поможет решить второе уравнение системы.

9.7.Из системы, полученной в результате замены, исключить свободные члены. Это приведет к уравнению, левую часть которого легко разложить на множители.

9.8.В качестве вспомогательного неизвестного удобно выбрать

9.9.Найти x и сделать проверку. Обратить внимание на то обстоятельство, что разность, стоящая в левой части данного уравнения, всегда положительна.

9.10.Второй путь удобнее, так как не приходится решать неравенство с параметром β, что значительно упрощает исследование.

9.14.Первое уравнение задает квадрат с центром в начале координат и с диагоналями, равными по длине 2, расположенными на координатных осях.

9.15.Ввести новые неизвестные: x + 1/ x = u , у + 1/ y = v .

9.16.В первое и второе уравнения входит разность у − z . Ее-то и следует исключить из этих уравнений.

9.17.Сумму x 4+ у 4в третьем уравнении удобно выразить через x ² + у ² и xу . В результате придем к уравнению относительно z .

9.18.Уравнение x + у = 1 − z позволит также упростить выражение, оказавшееся в скобках после того, как в третьем уравнении был вынесен за скобку множитель 1 − z .

9.19.Поскольку а , b и с — корни многочлена M ( t ), его можно записать в виде M ( t ) = ( t − а )( t − b )( t − с ). Приравняв коэффициенты при одинаковых степенях t в двух выражениях для M ( t ), найдем u , v и w (см. указание I, с. 138). Постарайтесь закончить решение, не прибегая к излишним выкладкам.

9.20.Умножить первое уравнение на xу ² z ², а второе на x ² уz ². Будет ли нарушена при этом равносильность?

9.22.Умножить первое уравнение на z и вычесть из второго. Аналогично поступить со вторым и третьим уравнениями.

9.23.Возвести первое уравнение в квадрат и вычесть его из второго. Из полученного уравнения исключить z , воспользовавшись сначала третьим, а затем первым уравнениями. (!!)

Чтобы осуществить эту операцию, первое уравнение нужно предварительно умножить на у .

9.24.Почленно сложить каждые два уравнения: первое и второе, первое и третье, второе и третье. Из найденной системы получить уравнение относительно u = xyz . (!!)

Чтобы получить уравнение относительно u = xyz , достаточно перемножить полученные уравнения.

9.25.Каждое уравнение — квадратное относительно соответствующего x k . Решив все эти квадратные уравнения и сложив их решения, мы получим уравнение относительно s . Гарантировать равносильность при этом нельзя, но в условии задачи требуется найти только одно решение.

9.26.Если обозначить 7 x − 11 у = u , то отсюда можно выразить z через u и у . Таким образом, мы получим снова систему двух уравнений с двумя неизвестными. Из этой системы легко исключить у .

9.27.Из такой системы можно исключить у , одновременно избавляясь от иррациональностей: нужно возвести оба уравнения в квадрат и вычесть второе из первого.

9.28.Выразить 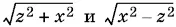через x и сравнить получающиеся в результате выражения для z ².

9.29.Полученная после возведения в квадрат система уравнений позволяет легко определить u − v , а затем u и v . (!!)

При определении u и v и при последующем вычислении x и у нужно провести исследование. В результате будут использованы условия а > b > 0 и а + b < 1, а также введенные при возведении в квадрат ограничения x > 0, у > 0.

9.30.Наряду с решением x 1, у 1, z 1у системы обязательно есть решение − x 1, − у 1, z 1. Таким образом, для единственности решения системы необходимо, чтобы эти два решения совпали. (!!)

Условие совпадения симметричных решений приведет к системе относительно а и b . Каждое из полученных значений а и b нужно проверить, так как мы воспользовались лишь необходимым условием единственности решения системы.

9.31.Подставив в первое и второе уравнения у = − x , мы получим два линейных уравнения относительно x ³. Выразить из каждого уравнения x ³ и приравнять эти два выражения. (!!)

Предыдущие рассуждения позволяют ограничить число рассматриваемых значений параметра а . Остается проверить, выполняются ли для каждого из оставшихся значений остальные условия задачи.

9.32.В качестве фиксированного значения b удобно выбрать b = 0. Мы придем к системе, из которой легко определить все возможные а . (!!)

Найденные значения а необходимо проверить.

9.33.Наряду с решением ( x 1, у 1) система имеет решение ( x 1, − у 1). Она может иметь единственное решение лишь при у = 0. Подставив это значение у , находим, что а = 0. Достаточно ли выполнение условия а = 0 для того, чтобы у системы было единственное решение?

9.34.После исключения 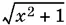получится уравнение

x ²/ y ²− 2 x / y + у ² + 2 x − 2 у = 3.

Его не следует преобразовывать в уравнение четвертой степени. Если в качестве вспомогательного неизвестного z взять некоторое выражение, содержащее x и у , то получится квадратное уравнение относительно z .