Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

3.38.Найти связь между радиусами шаров и величинами H , ρ и p можно, рассмотрев осевое сечение конуса.

3.39.Если рассмотреть осевое сечение обоих конусов, то задача станет плоской. Чтобы связать радиусы оснований конусов, в качестве вспомогательной величины удобно выбрать радиус сферы.

3.40.Сделав аналогичные построения для второй сферы, можно будет заключить, что, во-первых, треугольник О 1 ВО 2равнобедренный и, во-вторых, SB — высота пирамиды, объем которой мы ищем. (!!)

Так как BC (постройте этот отрезок на рис. I.3.40) (см. с. 129) — сторона основания правильной пирамиды, то можно доказать, что отрезок прямой EO 1является в треугольнике BEC одновременно медианой и биссектрисой. Это может оказаться полезным при вычислениях.

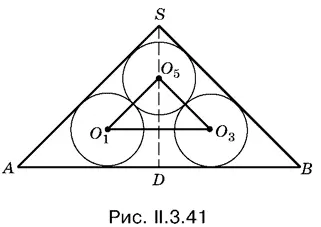
3.41.В осевом сечении, проходящем через О 1и О 3, получим картину, изображенную на рис. II.3.41. Все стороны треугольника О 1 О 3 О 5нам известны ( О 1 О 3легко найти из рис. I.3.41) (см. с. 129). Остается определить SD и AD .

3.42.Треугольники ASD и EMK подобны, т. е. углы SAD и MEK равны. Котангенс угла SAD нам известен, так как AD = a , SD = h . (!!)

Из треугольника SDC можно найти радиус основания цилиндра, а затем из треугольника EMK определить EK .

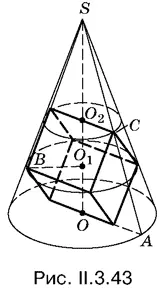
3.43.Рассмотреть подобные треугольники SOA и SO 1 B , где О 1— центр куба, а B — одна из вершин диагонального сечения куба, параллельного плоскости основания конуса. Это позволит найти одно соотношение между ребром куба а , высотой конуса H и радиусом его основания R (рис. II.3.43). (!!)

Второе соотношение между H , R и а можно будет найти, рассмотрев вторую пару подобных треугольников: SO 1 B и SO 2 C . Здесь О 2— середина верхнего ребра куба, а C — одна из вершин этого ребра. Имея в распоряжении два уравнения, можно выразить R и H через а и тем самым решить задачу.

3.44.В предыдущих рассуждениях не использовано условие, согласно которому три стороны трапеции, являющейся боковой гранью пирамиды, равны b . С помощью этого условия можно найти другое выражение площади боковой грани через а и b и приравнять первому. (!!)

Решить полученное однородное уравнение относительно а / b . Остается связать величину b с радиусом вписанного шара. Для этого достаточно рассмотреть треугольник, получающийся при проецировании одной вершины верхнего основания на нижнее.

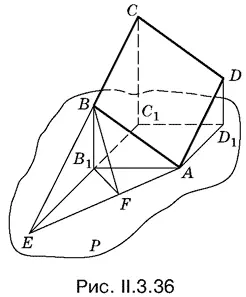
3.45.Обозначим через О 1и O 2центры меньших шаров, через O 3— центр большего шара, через О — центр шара, радиус которого нужно найти (рис. 11.3.45); Р 1 Р 2, Р 3, P — соответственно точки касания этих шаров с плоскостью. Радиус искомого шара обозначим через x . Тогда известны длины изображенных на рисунке отрезков: О 1 Р 1= O 2 Р 2= r , O 3 Р 3= R , ОР = x , O 1 O 2= 2 r , O 1 O 3= O 2 O 3= R + r , OO 1= OO 2= r + x , OO 3= R + x . Мы считаем очевидным, что x < r . (!!)

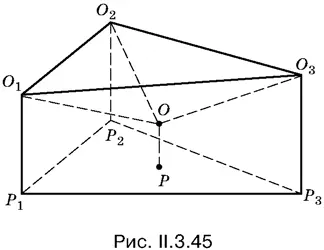
Нужно найти соотношение, связывающее величины R , r и x . Для этого придется рассмотреть треугольник Р 1 Р 2 Р 3и вычислить длины проекций отрезков, соединяющих центры шаров. Так как шары O 1и O 2равны, то O 2 O 3= O 1 O 3и, следовательно, Р 2 Р 3= Р 1 Р 3. Поэтому точка P лежит на высоте и медиане равнобедренного треугольника Р 1 Р 2 Р 3.

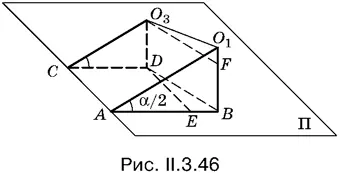
3.46.Обозначим через O 1центр одного из двух равных шаров, а через O 3— центр меньшего шара. Пусть эти шары касаются нижней грани двугранного угла (рис. 11.3.46) в точках В и D соответственно. Прямоугольные треугольники O 1 АВ и O 3 CD имеют углы при вершинах А и С , равные α/ 2. Чтобы использовать факт касания шаров O 1и O 3и наличие у них общей касательной плоскости Π, нужно рассмотреть треугольник O 1 O 3 F , в котором О 1 О 3= R + r ( R — радиус большего шара, r — радиус меньшего шара), O 1 F = R − r ( F — проекция точки О 3на отрезок О 1 В ). Если удастся выразить O 3 F через R , r и α, то мы получим соотношение, позволяющее определить угол α. (!!)

Отрезок O 3 F (см. рис. II.3.46) равен ВD , а ВD можно выразить через катеты прямоугольного треугольника ВDЕ , где E — проекция точки D на отрезок AB . Чтобы найти ЕD , нужно воспользоваться фактом касания шаров О 1и О 2, сделайте на рисунке необходимые построения, рассмотрев проекцию их линии центров на плоскость Π.

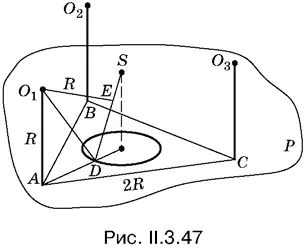
3.47.Так как каждый из трех шаров с центрами в точках О 1, О 2, О 3касается боковой поверхности конуса и плоскости P , то длина перпендикуляра, опущенного из центра шара на плоскость P , равна длине перпендикуляра, опущенного из центра на ближайшую к нему образующую (рис. II.3.47).

3.48. Оси двух соседних конусов и их общая образующая лежат в одной плоскости (докажите). Рисунок, сделанный в предположении, что ось конуса и две образующие, по которым происходит касание с соседними конусами, лежат в одной плоскости, будет неверным. При таком расположении конусов касание происходило бы по диаметрально противоположным образующим, т. е. основание конуса было бы перпендикулярно к плоскости, и общая вершина конусов не смогла бы лежать в этой плоскости. (!!)

Угол между осями соседних конусов искомый.

3.49.Центр сферы, построенной на AB , обозначим через О 1, а центр вписанной сферы — через О 2. Пусть F — точка касания сферы О 2с гранью САD . Треугольники FO 2 A и OKA подобны.

3.50.Плоскость, проведенная через ось РР и точку О — центр основания пирамиды (обозначим ее через Π), разобьет пирамиду SАВСD на две равные части, расположенные симметрично относительно этой плоскости. Вместо всей пирамиды можно вращать вокруг РР одну из этих частей. Теперь нужно заменить пирамиду плоской пластинкой, дающей при вращении то же тело, что и пирамида. Для этого каждое из сечений SEF пирамиды нужно перенести с помощью поворота в плоскость Π. (!!)