Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

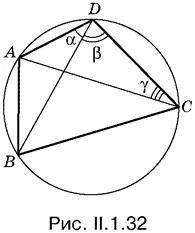
1.32.Чтобы выразить все участвующие в формулировке задачи величины через R и синусы соответствующих углов, нужно ввести углы так, как это показано на рис. II. 1.32, и затем воспользоваться теоремой синусов.

1.33.При продолжении боковой стороны трапеции и указанного в условии отрезка до их пересечения получаются подобные треугольники. Это позволяет выписать соответствующую пропорцию и составить из нее производную пропорцию.

1.34.Чтобы использовать условие AN : NB = 1 : 2, можно отметить на рисунке точку пересечения прямой с продолжением одной из сторон квадрата или провести через точку N прямую, параллельную BC .

1.35.Чтобы составить уравнение относительно x , удобно выразить через x отрезок АЕ один раз с помощью квадрата, а другой раз с помощью треугольника.

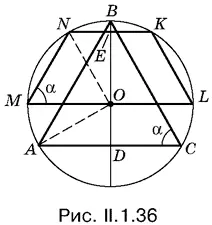
1.36.Чтобы связать треугольник и трапецию с окружностью, естественно провести радиусы в вершины обеих фигур. K этим радиусам прилегают прямоугольные треугольники. Выясните, какие из них равны. (!!)

Углы NOE и OAD (рис. II.1.36) можно выразить через угол а и убедиться в том, что они равны.

1.38.Выразить через R и n периметры первого и второго многоугольников и сравнить с периметром третьего многоугольника.

1.39.Величину R можно вычислить, построив треугольник, в котором все стороны выражаются через R и известные величины. В качестве такого треугольника удобно выбрать треугольник ОМО 1, где О 1— центр рассматриваемой в задаче окружности.

1.40.Ввести в рассмотрение угол ADC (обозначить его через φ) и равный ему угол BEC . Найти tg φ.

1.41.Чтобы применить к треугольнику AOO 1теорему косинусов, придется использовать угол β между хордой AB и диаметром, исходящим из точки А . Косинус и синус этого угла легко выразить через b и r .

1.42.Чтобы использовать условие задачи, нужно соединить центр окружностей с концами и серединами хорд, являющихся сторонами квадрата. При решении следует помнить, что возможны два варианта взаимного расположения квадрата и центра окружностей: либо центр лежит внутри квадрата, либо вне его.

1.43.Чтобы составить уравнение относительно x , рассмотрите треугольник ОЕС , в котором все стороны можно выразить через R и x .

1.44.Ввести обозначения R , r и x , где x — расстояние между проекциями центров на нижнее основание. Составить уравнения, используя условия задачи и теорему Пифагора.

1.45.Чтобы доказать, что фигуры СQNK и ОQR равновелики, достаточно доказать, что равновелики секторы COQ и KDN . Для этого следует выяснить связь между радиусами большей и меньшей окружностей.

1.46.Пусть K — проекция точки O на AB . Отрезок OK можно вычислить двумя способами: из треугольника OAK и из треугольника OKP 1.

1.47.Так как хорды пересекаются внутри окружности, то естественно воспользоваться равенством произведений отрезков, на которые каждая хорда делится точкой пересечения.

1.48.Чтобы связать x и R , а именно это требуется в условии задачи, нужно опустить из центра О 2перпендикуляры O 2 D и О 2 С на радиусы OA и ОВ соответственно.

Рассмотреть треугольник О 2 СО 1. Выразить О 2 С через x и R , используя тот факт, что угол ОАВ = 45°.

1.49.Угол АМС равен π − 2φ. Если МВ = МС = рx , то AC можно выразить из треугольников АМС и АВС . Приравняв эти выражения, получим уравнение относительно x .

1.50.Если стороны треугольника а , а − d , а + d , то его полупериметр p = 3 a / 2 . Из формулы Герона получим уравнение относительно а :

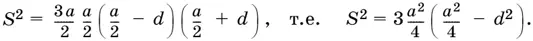
Это уравнение нужно решить относительно а . Подберите удобную замену переменной.

1.51.Пусть PP 1— средняя линия треугольника АВС , а QQ 1— средняя линия треугольника PBP 1Пусть далее P 1— точка пересечения PP 1и BR , а Q 2— точка пересечения QQ 1с BR . Убедитесь в подобии треугольников Р 2 TP и Q 2 TQ .

1.52.Рассмотрите треугольники с общей вершиной, опирающейся на отрезки, которые участвуют либо в условии задачи, либо в искомом соотношении.

1.53. MN — хорда второй окружности, ее центральный угол МО 2 N равен 150°, что следует из рассмотрения первой окружности.

1.54.Так как α + β + γ+ δ = 180°, то площадь S четырехугольника АВСD равна

S = ½ ab sin (γ + δ) + ½ cd sin (α + β) = ½ sin (α + β) ( ab + cd ).

Далее воспользоваться теоремой синусов, в силу которой а = 2 R sin α, b = 2 R sin β , ... .

2.1.Осуществить параллельный перенос отрезка DC в точку В .

2.2.Сколько решений имеет задача?

2.3.Точки А и А 1лежат на прямой, параллельной BC и отстоящей от BC на расстоянии h а . Нужно найти еще одно свойство любой из этих точек; в этом должен помочь угол φ.

Отразив треугольник СА 1 А от оси А 1 А , получим треугольник С 1 А 1 А (рисунок сделайте самостоятельно). Фигура С 1 АВА 1— параллелограмм, у которого вершины С 1и В фиксированы, углы известны, а две другие вершины нужно построить.

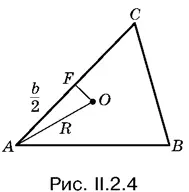
2.4.Зная R и b , можно построить треугольник АОF (рис. II.2.4). Остается использовать медиану m с . Чтобы это сделать, нужно, после того как построен треугольник АОF , построить середину отрезка AB .

2.5.Докажите, что точка Q лежит на окружности, описанной около треугольника АВС . Для этого достаточно вычислить угол ВО 1 С .

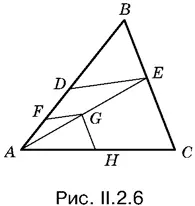
2.6.Предположим, что точки D и E найдены (рис. II.2.6). Если через любую точку F , лежащую на AB , провести прямую FG , параллельную DЕ и пересекающую АЕ в точке G , а через точку G — прямую GH , параллельную ЕС , то получим четырехугольник AFGH , подобный АDЕС , с центром подобия в точке А .

2.7.«Средним» будет такое положение прямой FЕ , когда FM = ME .