Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

1.6.Из данного соотношения между площадями треугольников АDС и АВD , имеющих общую сторону АD и одинаковые углы при вершине А (поскольку АD — биссектриса треугольника АВС ), можно найти отношение сторон AC : AB . Далее применить теорему синусов.

1.7.Площадь треугольника САD ( D — точка пересечения биссектрисы внешнего угла А треугольника АВС с продолжением стороны СВ ) можно вычислить двумя способами, используя лишь элементы, участвующие в задаче.

1.8.Сумма двух сторон треугольника, не лежащих против угла А , участвует в выражении площади через полупериметр и радиус вписанной окружности и в выражении через биссектрису и синус половинного угла. Из этих двух выражений сумму b + с нужно исключить.

1.9.Отношение отрезков АО и ОМ дано. Эти отрезки можно рассматривать как отрезки, на которые сторона AM треугольника АВМ делится биссектрисой ВО . В результате мы перейдем к отношению отрезков AB и ВМ , последний из которых легко выражается через стороны данного треугольника.

Аналогично нужно поступить с отношением отрезков ВО и ON .

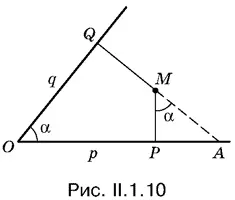
1.10.Угол РМА равен углу QОА (рис. II.1.10). Чтобы найти МР , нужно рассмотреть сначала треугольник РМА , а затем треугольник ОАQ .

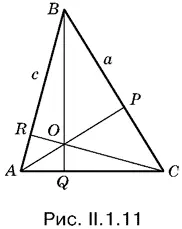
1.11.С помощью первого указания можно получить одно уравнение, связывающее углы данного треугольника. Ко второму уравнению нас приведет условие, в силу которого высота ВQ треугольника АВС (рис. II.1.11) в 6 раз больше высоты ОQ треугольника АОС . Достаточно выразить АQ из треугольников АВQ и АОQ , заметив при этом, что угол ОАQ является дополнительным для угла С .

1.12.После того как получено соотношение

h / sin C + h / sin B = k

использовать условие, согласно которому В − С = π/ 2, с тем, чтобы получить уравнение относительно одной тригонометрической функции неизвестного угла С . Для достижения этой цели можно, например, в написанное выше соотношение подставить В = π/ 2+ С . После этого полученное соотношение удобно возвести в квадрат.

1.13. Способ 1.Через x , y и z можно выразить площадь треугольника:

ха + yb + zc = 2 S .

Еще три соотношения, в которых участвуют x , y и z , получим, если выразим каждый из отрезков АО , ВО и СО из двух прилегающих к нему треугольников.

Способ 2.Связать отрезки l , m и n удобно с помощью теоремы косинусов для каждого из трех треугольников АОВ , АОС и ВОС , сумма площадей которых равна площади треугольника АВС .

1.14.Остается использовать условие, что А − В = φ. С помощью формул преобразования произведения тригонометрических функций в сумму придем к тригонометрическому уравнению относительно A + B / 2.

1.15.Площадь треугольника АВС , которую мы временно обозначим через S , равна

S = ½ ah a = ½ bh b .

Кроме того, S выражается через а , b , l и sin C / 2, если треугольник АВС разделить биссектрисой СD на два треугольника.

1.16.Для нахождения угла СОВ следует использовать тот факт, что центр вписанной в треугольник окружности лежит на пересечении биссектрис. Для этого нужно выразить ∠ СОВ через сумму ∠ ОСВ + ∠ ОВС .

1.17.Так как по условию стороны треугольника образуют арифметическую прогрессию, то обозначим их длины через а , а + d , а + 2 d и постараемся связать радиус вписанной окружности с длинами сторон. На рисунке треугольник удобно расположить так, чтобы средняя по длине сторона оказалась его основанием.

С помощью сравнения площадей легко выразить высоту треугольника через радиус вписанной окружности. Этот факт будет полезен для исследования образовавшихся подобных треугольников.

1.18.Заметить, что проекция отрезка АО ( О — центр вписанной окружности) на сторону b равна p − а.

1.19.Чтобы доказать, что треугольники АВС и OKL подобны, достаточно установить равенство их углов. Так как углы треугольника АВС легко выражаются через угол С , то и углы треугольника OLK тоже следует постараться выразить через тот же угол С . Начать удобно с угла KOL , который равен углу АОВ .

1.20.Чтобы связать стороны треугольника и его углы, удобно воспользоваться теоремой синусов; так как соотношение, которое нужно доказать, однородно, линейные элементы сократятся.

1.21.Если через одну из вершин треугольника АВС провести отрезок, параллельный противоположной стороне треугольника до пересечения с данной в условии прямой, то получим нужные подобные треугольники.

1.22.Если в треугольнике АВС провести высоту АЕ , то получим три прямоугольных треугольника; с помощью теоремы Пифагора АВ ², АС ² и АD ² можно выразить через АЕ и отрезки, лежащие на BC .

1.23.Если AC — основание треугольника, то дополнительное построение удобно выполнить так: через вершины А и С провести прямые, параллельные ВQ , а отрезки СR и АР продолжить до пересечения с этими прямыми. В результате возникнут все необходимые для решения подобные треугольники.

1.25.В качестве неподвижного радиуса удобно выбрать АО . Сумму квадратов расстояний выразить через радиус R описанной около треугольника окружности и угол α.

1.26.Две стороны треугольника и угол между ними известны. Третью сторону можно найти по теореме косинусов, а радиус описанной окружности — по теореме синусов.

1.27.Выразить cos А и cos С через стороны треугольника и сравнить cos 2 С с cos А , имея в виду данное в условии соотношение: а ² = с ( b + с ).

1.30.Сделать это можно так: ВЕ будет стороной, соответствующей О 1 Е , а через точку E нужно будет провести прямую, параллельную KO 2, и отложить на ней отрезок, равный KO 2.

1.31.Достроить треугольник АВС до параллелограмма так, чтобы сторона AB была диагональю этого параллелограмма, а через вершину В провести ВD 1‖ АD . Рассматривая треугольник МDС и подобный ему треугольник с вершинами в точках В и С , найдем отношение, в котором точка M делит отрезок АD .