Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

23.4.Найдя область определения функции arccos ( x ² − 3 x + 1), исключить точки, в которых не существует tg 2 x . (!)

23.5.Решить графически систему неравенств, обеспечивающих существование данного выражения. (!)

23.6. Способ 1.Доказательство можно вести от противного, предположив, что функция имеет период T .

Способ 2.Найти корни функции и исследовать их в предположении, что у функции имеется период.

23.7.Записать тождество, равносильное условию, что f ( x ) имеет своим периодом число T . Рассмотреть это тождество при x = 0 и x = ± T . (!)

23.8.Ясно, что любое общее кратное периодов cos 3 x / 2 и sin x / 3будет периодом данной функции. Доказать, что наименьшее общее кратное будет основным периодом.

24.1.Заменить cos² x на 1 − sin² x. В результате получится квадратный трехчлен относительно sin x .

24.2.Записать у как одну функцию другого аргумента.

24.3.Привести к одной тригонометрической функции другого аргумента.

24.4.Выражение можно представить в виде А ² + В ² + С , где С — константа.

24.5.Чтобы раскрыть знаки абсолютных величин, нужно нанести на числовую ось точки ±1 и ±2, которые разобьют ее на пять интервалов.

24.6.Воспользоваться неравенством между средним арифметическим и средним геометрическим нескольких чисел.

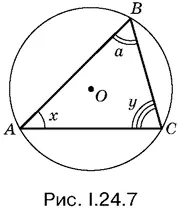
24.7.Чтобы найти максимум AB + BC , удобно ввести углы x и у (рис. 1.24.7), имея в виду, что x + у = π − α, и перейти с помощью теоремы синусов к тригонометрическим соотношениям. (!)

24.8.Если обозначить катеты основания через а и b , то боковая поверхность призмы равна

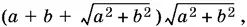
причем ab = 4.

24.9.Квадрат должен быть вписан в шестиугольник так, чтобы не нарушалась симметрия, т. е. центр квадрата должен совпадать с центром шестиугольника.

24.10.Прежде всего необходимо обратить внимание на свойства квадратного трехчлена, стоящего в знаменателе. Его дискриминант отрицателен и, следовательно, трехчлен не может быть равен нулю при действительных x .

Если обозначить теперь данную дробь через у , то можно получить квадратное уравнение относительно x , в котором у играет роль параметра.

24.11.Если ребра параллелепипеда обозначить через а , b и с , то условие задачи можно записать в виде системы

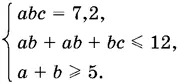
Из второго и третьего неравенств следует, что

ab + с ( а + b ) ≥ ab + 5 с .

24.12.Чтобы найти наименьшее значение этой функции, естественно выделить полный квадрат. Однако удобнее вначале перейти от котангенсов к косекансам, что позволяет выразить функцию только через синусы:

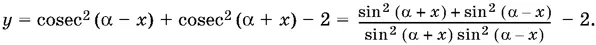
Теперь в числителе следует выделить полный квадрат разности. При этом могут представиться два случая, в зависимости от знака произведения sin (α + x) sin (α − x). Чтобы не рассматривать их отдельно, можно необходимые преобразования записать так:

sin² (α + x ) + sin² (α − x ) = [|sin (α + x )| − |sin (α − x )|]² + 2 |sin (α + x) sin (α − x)|.

24.13.Известно, что arcsin x + arccos x = π/ 2. Поэтому данную функцию удобно преобразовать так, чтобы воспользоваться этим соотношением.

24.14.Воспользоваться преобразованием нормирования:

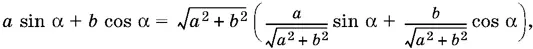
после чего коэффициенты при sin α и cos α можно объявить косинусом и синусом общего аргумента φ, т. е.

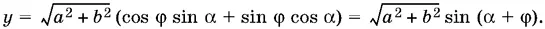
Функция у достигает своего наименьшего значения

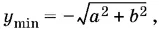
когда sin (α + φ) = −1, и наибольшего значения

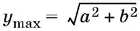
при sin (α + φ) = 1. (!)

24.15.Систему естественно привести к виду

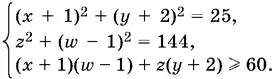
Свободные члены равны, соответственно, 5², 12² и 5 · 12. Удобно каждое из соотношений разделить на его свободный член.

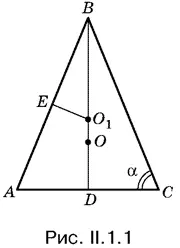
1.1.Из треугольника AO 1 D определить АO 1;если известен радиус окружности O 1(см. рис. I.1.1 на с. 114).

1.2.Зная AB , можно найти AD и радиус ВО 1описанной окружности (рис. II.1.2 [15] Так в тексте. От верстальщика fb2. ). Нужно лишь заметить, что угол ABD равен π/ 2− α, а ВE = АB / 2.

1.3.Возможны два случая взаимного расположения треугольника и окружности. Либо окружность будет вписана в треугольник так, что каждая точка касания делит соответствующую сторону пополам, либо одна вершина треугольника окажется внутри окружности, а две другие — вне.

Найдите решение, не зависящее от взаимного расположения окружности и треугольника. Для этого достаточно рассмотреть треугольник, который получится, если соединить середины сторон данного треугольника.

1.4.Чтобы найти отношение площадей треугольников А 1 В 1 С и АВС , нужно применить теорему об отношении площадей треугольников, имеющих равный угол.

В обозначениях, введенных на рис. II.1.4. имеем

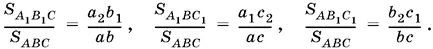
С помощью теоремы о биссектрисе внутреннего угла треугольника остается выразить а 1, a 2, b 1, b 2, c 1, с 2через а , b и с .

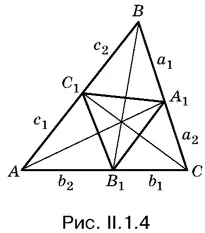
1.5.Если центр вписанной в треугольник окружности обозначить через О , то площадь треугольника АВС можно будет вычислить как сумму площадей треугольников АОВ , ВОС и СОА . При этом каждая из сторон АО , ВО и СО может быть выражена через радиус r вписанной окружности. Площадь треугольника А 1 В 1 С 1тоже разбивается на три площади: А 1 ОВ 1, В 1 ОС 1и С 1 ОА 1. Остается углы А 1 ОВ 1, В 1 ОС 1и С 1 ОА 1выразить через углы треугольника АВС .