Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

16.12.Данную систему нужно заменить системой без логарифмов. Однако при этом следует помнить обо всех ограничениях, которые накладываются на число, стоящее под знаком логарифма, и на основание логарифма.

16.13.Уравнение составлено таким образом, что решить его с помощью элементарных преобразований нельзя. Остаются два пути: либо графическое решение, либо оценка правой и левой частей уравнения. Второй путь предпочтительнее, так как левая часть легко оценивается, если положить 4 cos² − π x = u .

16.14.Трехчлен x ² − x + 0,5 всегда больше 0,25.

17.1.Данную систему решить относительно f (2 x + 1) и g ( x − 1).

17.2. f ( x ) = x ( x ² − 6 x + 9) = x ( x − 3)²,

f ( f ( x )) = f ( x ) ( f ( x ) − 3)² = x ( x − 3)²( x ³ − 6 x ² + 9 x − 3)².

17.3.Из второго уравнения найти 2 и подставить в первое. Воспользоваться условием, что x и у — целые числа.

17.4.Неравенство | x + 2| ≤ x + 2 удовлетворяется при всех x ≥ −2.

Уравнение следует преобразовать с помощью подстановки

2 x − 1= у , sin π x / 2= 2.

17.5.Найти первообразную F ( x ) и воспользоваться условием касания графиков функций f ( x ) и F ( x ) в некоторой точке F 0( x 0; у 0).

17.6.Данное неравенство равносильно такому:

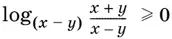
Рассмотрите случаи: а) 0 < x − у < 1 и б) x − у > 1.

17.7.Изобразите на графике часть плоскости, координаты точек которой удовлетворяют первому неравенству, для каждого квадранта отдельно. Для первого квадранта это будут все его точки.

17.8.Начать нужно с определения координат точки E . Для этого придется записать уравнение прямой, проходящей через две точки ( x 1, у 1) и ( x 2, у 2):

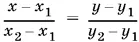
сначала для точек В и D , затем для точек А и C . Решение системы этих двух уравнений даст нам координаты точки E .

17.9.Оба неравенства зависят от x + у и от у − x . Это подсказка побуждает ввести новые переменные u = x + у и v = у − x .

17.10.Если x 1и x 2— целые, то и а — целое. (Докажите.)

17.11.Это биквадратное уравнение, и оно сводится к квадратному подстановкой x ² = у . Знак дискриминанта квадратного уравнения не позволяет ответить на вопрос о числе корней исходного уравнения. Нужно позаботиться, чтобы у ≥ 0.

17.12.Поскольку cos 8 x = 1 − 2 sin² 4 x , исходное уравнение преобразуется в квадратное относительно у = sin 4 x , где | у | ≤ 1.

17.13. Подставив любые значения x и а в данное уравнение, получим соответствующее единственное значение у . Таким образом, при любом фиксированном а любая прямая, параллельная оси у , пересечет кривую семейства, соответствующую этому а , в единственной точке. Это не означает, что через каждую точку плоскости ( x , у ) проходит кривая семейства. Не при любом у мы найдем точки плоскости ( x , у ), соответствующие данному семейству.

18.1.Если ввести в качестве неизвестных производительности труб, то получим три уравнения с четырьмя неизвестными (объем бассейна следует принять за единицу).

18.2.Если плечи весов равны l 1и l 2, то можно вычислить массу P товара, отпущенного покупателю.

18.3.Эта задача менее всего похожа на «алгебраическую». Скорее, она напоминает рассуждения человека, пытающегося обнаружить факт на основе отрывочных сведений. Вначале следует обратить внимание на то обстоятельство, что листов в альбоме — число целое. После этого нужно использовать условие задачи с тем, чтобы ограничить рассмотрением возможные значения этой переменной.

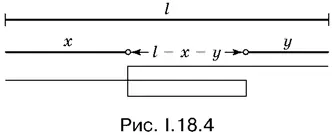
18.4.Путь буксира изображен на рис. 1.18.4, где x — часть пути, которую прошел самостоятельно (т. е. без буксировки) первый понтон, а y — часть пути, которую прошел без буксировки второй понтон.

18.5.Так как некто родился в девятнадцатом веке, то неизвестны две последние цифры его года рождения. Если мы обозначим их через x и y , то сможем записать условия задачи в виде уравнений.

18.6.Если одна часть имеет массу x карат, то ее цена lx ², где l — коэффициент пропорциональности.

18.7.Основная трудность в выборе неизвестных, которые позволили бы связать данные в условии величины. Здесь эту роль могут выполнить нормы расхода горючего при работе двигателя с фиксированной собственной скоростью. K чему удобнее отнести эти нормы: к часу работы двигателя или к километру пути в стоячей воде?

18.8.Выбор неизвестных подсказан условием задачи: x , y , z , s и t — число десятков порций соответствующих сортов мороженого. Выбрав в качестве неизвестных число десятков порций, а не число самих порций, и заметив, что неизвестные — натуральные числа, мы тем самым использовали условие, в силу которого у продавца есть по нескольку десятков порций мороженого. Последнее условие задачи запишется в виде неравенства y > s . Это ограничение позволит нам восполнить отсутствие пятого уравнения в системе с пятью неизвестными.

18.9.Пусть С — устье реки. Время, за которое плоты прошли весь путь от А до В , известно, а время, за которое прошли путь СB , обозначим через x . Если ввести в рассмотрение расстояние AC , то скорость течения реки можно выразить из остальных условий задачи.

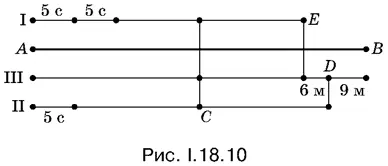
18.10.Условия задачи отражены на схеме (рис. 1.18.10). С помощью схемы можно составить четыре уравнения: встреча в точке С дает два уравнения и две оставшиеся встречи — по одному.

18.11.Вначале нужно проследить весь процесс за один цикл в предположении, что объем сосуда принят за единицу, а часть его объема, занимаемая раствором, обозначена через x .

18.12.В качестве неизвестных удобно выбрать: x — скорость автомобиля, y — скорость мотоцикла и z — расстояние между пунктами А и В . Первая встреча произошла через z / x + у ч после начала движения на расстоянии zy / x + у км от пункта В .