Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы
- Название:Сборник задач по математике с решениями для поступающих в вузы
- Автор:
- Жанр:
- Издательство:«ОНИКС 21 век» «Мир и Образование»
- Год:2003
- Город:Москва
- ISBN:5-329-00766-6, 5-94666-080-2
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы краткое содержание
Основу задачника составили варианты письменных работ по математике, предлагавшихся на вступительных экзаменах в ряде ведущих вузов Москвы.
Сборник содержит около 500 типовых задач. K каждой задаче дается до трех указаний, помогающих найти правильный путь к решению, а затем приводится подробное решение.
Пособие может использоваться при самостоятельной подготовке к экзаменам в вуз, а также на подготовительных отделениях и курсах.
Сборник задач по математике с решениями для поступающих в вузы - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
13.11.Рассмотреть случаи, позволяющие раскрыть знаки абсолютной величины; задача сведется к решению двух уравнений и к выбору тех значений x , которые попадают в указанный интервал.
13.12.Вначале следует посмотреть, не стоит ли под радикалом полный квадрат какого-то выражения. Число 16 нам, скорее всего, не помешает, а вот число 17 менее удобно для последующих преобразований. Чтобы освободиться от его присутствия, удобно вынести под радикалом sec² x за скобки, а оставшееся в скобках выражение записать через sin x .
13.13.Перенести все члены уравнения в левую часть и разложить на множители с тем, чтобы появилась возможность избавиться от большинства радикалов.
13.14.Выразить sin 4 x через tg 2 x . Это тождество условное, поэтому нужно убедиться в равносильности полученного уравнения данному.
13.15.Перейти к функциям sin x и cos x .
13.16.Правую часть уравнения можно сократить на cos 2 x , добавив условие cos 2 x ≠ 0.
13.17.С помощью универсальной подстановки (через тангенс половинного угла) это уравнение может быть сведено к кубичному уравнению относительно у = tg x / 2. Равносильное ли получится уравнение?
13.18.Понизить степень.
13.19.Левую и правую части можно привести к виду, удобному для логарифмирования.
13.20.Уравнение упростится, если преобразовать произведения, стоящие в левой его части, в разность косинусов. Оно станет квадратным относительно у = cos x . (!)
13.21.Выразить sin 4 x через sin x и cos x и вынести sin x за скобки после переноса в левую часть.
13.22.Раскрыть скобки и каждое из ста произведений преобразовать в сумму. (!)
13.23.Каждое произведение преобразовать в разность косинусов. (!)
13.24.Выразить cos 4 x + 1 через cos 2 x .
13.25.Произведение косинусов может равняться единице, если либо оба косинуса равны единице, либо оба равны минус единице.
13.26.Представить единицу в виде sin² x + cos² x .
13.27.Уравнение таково, что не остается надежд на упрощения в результате тригонометрических преобразований. Поэтому следует попытаться воспользоваться оценками. Во-первых, выражение, стоящее в левой части, всегда неотрицательно, кроме того, cos 4 x ≥ 0; следовательно, и cos 3 x ≥ 0. Во-вторых, слева стоит сумма квадратов, которую разумно дополнить до полного квадрата.
13.28.Обратить внимание на то обстоятельство, что левая часть уравнения не может стать меньше единицы, а правая не может превзойти единицу.
13.29.Второе уравнение легко свести к виду sin (2 x − у ) = 0, откуда у = 2 x − π k . При подстановке в первое уравнение получим
4 tg 3 x = 3 tg 4 x .
Это уравнение удобнее преобразовать к виду
4(tg 4 x − tg 3 x ) = tg 4 x ,
чем к виду
3(tg 4 x − tg 3 x ) = tg 3 x ,
так как множитель 4 удобнее при тригонометрических преобразованиях.
13.30.Второе уравнение легко решается преобразованием его левой части в разность косинусов; в результате получится соотношение 2 у = π/ 2− x + k π. Прежде чем им воспользоваться, следует первое уравнение привести к виду, удобному для логарифмирования.
13.31.Левые части первого и второго уравнений нетрудно выразить через u = sin x и v = sin у .
13.32.Второе уравнение существенно упростится, если его левую часть преобразовать в сумму.
13.33.Из системы можно исключить x , если воспользоваться основным тригонометрическим тождеством
sin² φ + cos² φ = 1.
13.34.Нужно вначале решить первое уравнение, решение которого находится обычным путем. Найденное значение подставить во второе уравнение.
13.35.Разделив второе уравнение на первое, получим tg у = 2 tg x .
13.36.Удобно перейти к уравнениям относительно одной тригонометрической функции. При этом нужно следить за равносильностью.
13.37.Если возвести каждое уравнение в квадрат и полученные уравнения сложить, то мы исключим α. Однако для нас важнее исключить либо x , либо у . Как это сделать?
13.38.Левую часть первого уравнения можно преобразовать в разность sin ( x − у ) − cos ( x + у ). Из второго уравнения определяется cos ( x + у ).
13.39.Правая часть уравнения не может стать больше четырех. Если ввести обозначения tg² x = u , tg² у = v , то нетрудно заметить, что левая его часть не может стать меньше четырех.
13.40. Способ 1.Умножить sin² x на тригонометрическую единицу sin² 3 x + cos² 3 x и сгруппировать члены, содержащие sin² 3 x .
Способ 2.Перенести все члены в левую часть и выделить полный квадрат разности 2 sin x − sin² 3 x . Оставшиеся члены образуют неотрицательное выражение.
13.41. Способ 1.Преобразовать сумму тригонометрических функций cos x + cos у в произведение, а cos ( x + у ) выразить через косинус половинного аргумента.
Способ 2.Раскрыть cos ( x + у ) по формуле косинуса суммы.
13.42.Вопрос задачи естественно поставить следующим образом: при каких а и b равенство
tg x + tg ( а − x ) + tg x tg ( а − x ) = b
является тождеством (неабсолютным)?
13.43.Вначале следует попытаться оценить снизу левую часть уравнения, так как верхняя оценка правой части очевидна:
12 + ½ sin у ≤ 12,5.
13.44.Перенести sin З x в левую часть уравнения и преобразовать sin x − sin З x к виду, удобному для логарифмирования.
13.45.После раскрытия скобок произвести упрощения.
13.46.Условие записано таким образом, что введение нового неизвестного
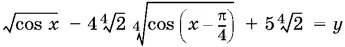
является очевидным шагом к решению уравнения. Мы придем к квадратному уравнению относительно у.
13.47.В задаче требуется решить систему двух уравнений с одним неизвестным и выбрать решения, удовлетворяющие ограничению | x | < 5. Было бы заблуждением пытаться свести эти два уравнения в одно с помощью подстановки или какого-либо другого преобразования. Можно решить каждое в отдельности и отыскать общие корни. Однако попытайтесь использовать особенности данной системы.
13.48.Так как выражений, схожих с cos 6 x / 5, в условии больше нет, то, скорее всего, cos 6 x / 5преобразовывать не следует. В числителе левой части tg x естественно вынести за скобки. Выражение 3 − tg² x , оставшееся в скобках, удобнее преобразовать, заменив tg² x на 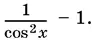
Интервал:
Закладка:










