Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

Теперь нетрудно подсчитать расстояние между пунктами первой и второй встречи.

18.13.В качестве неизвестных удобно выбрать расстояние ( x ), которое пассажир проехал на такси и ( y ) на автобусе, скорость поезда ( u ) и время, на которое пассажир опоздал на поезд ( t ).

18.14.Скорости поездов связаны со всеми величинами, участвующими в задаче. Поэтому естественно ввести в качестве неизвестного x скорость товарного поезда до остановки. Тогда mx — скорость пассажирского поезда до остановки.

Однако одного неизвестного здесь мало, так как поезда выходили из своих пунктов в разное время. Чтобы связать скорости и времена, нам нужно ввести в рассмотрение расстояния. Пусть расстояние между А и В равно y , а расстояние между А и С равно z .

18.15.Вопрос задачи не имеет прямого отношения к ее решению. Поэтому величину, о которой спрашивается в задаче, не следует выбирать в качестве неизвестного, так как она сложно связана с остальными компонентами. Наиболее удачно связать участвующие в задаче величины — расстояния и промежутки времени — можно с помощью скоростей самолета и вертолета.

18.16.Если обозначить устье реки, на которой стоит порт M , буквой А , а устье второй реки буквой В , то для решения задачи удобно ввести два неизвестных расстояния. Сразу же появляется желание обозначить расстояние AB , которое требуется определить, буквой x , один из оставшихся отрезков, МА или NA , — буквой у , а последний отрезок записать как s − ( x + у ). Однако более естественно не нарушать симметрию и обозначить буквами x и у отрезки МА и BN соответственно. Тогда отрезок AB будет равен s − ( x + у ). Поскольку нас интересует только отрезок AB , то нужно определить x + у .

18.17.Поскольку линейные единицы измерения в условие не входят, целесообразно принять расстояние между А и В за единицу. Если ввести скорости поездов: u — скорого, v — пассажирского, 2 v — курьерского, то легко определить u в долях AB в час.

18.18.Первый вопрос, который должен возникнуть у хозяйственника, решающего подобную задачу, какой из комплектов выгоднее заказать, т. е. для какого из них средние расходы на пересылку одной детали будут наименьшими.

19.1.Записать выражения для и n и и n + 1и сравнить.

19.2.Поскольку первый член арифметической прогрессии входит в качестве слагаемого в выражения для любого ее члена, удобнее сразу записать a q − а р , a r − a q , a s − а z . Это тем более удобно, что нас интересуют разности p − q , q − r , r − s .

19.3.Если ввести а 1и u 1— соответственно первые члены арифметической прогрессии с разностью d и геометрической прогрессии со знаменателем q , то а , b и с придется выразить через а 1, u 1, d и q .

19.4.В левой части удобно перейти к общему основанию x .

19.5.Если бы сумма состояла из одних девяток, то каждый член можно было бы представить в виде 10 k − 1.

19.6.Выражение, стоящее под знаком квадратного корня, умножить и разделить на 9. Число, состоящее из k девяток, равно 10 k − 1.

19.7.Условия задачи можно записать в виде а 1+ а 3= 2 а 2, а 1 а 3= а 2² . Из этой системы нетрудно исключить а 2.

19.8.Удобно ввести знаменатель прогрессии q и с его помощью записать теорему Виета для обоих уравнений. Это позволит определить q и x 1. (!)

19.9.Так как корни уравнения образуют геометрическую прогрессию, то x 2= x 1 q , x 3= x 1 q ². Воспользуйтесь теоремой Виета для уравнения третьей степени.

19.10.Если приравнять выражения для удвоенной суммы n членов прогрессии и суммы всех ее членов, то получим уравнение относительно q n .

19.11.Так как число делится на 45, то оно может оканчиваться либо нулем, либо пятью. Рассмотреть эти два случая.

19.12.Если обозначить через x цифру единиц, а через q — знаменатель прогрессии, то легко составить два уравнения, отражающих условия задачи. Однако можно пойти по другому пути: поскольку цифры числа образуют геометрическую прогрессию и само число больше 594, то в нашем распоряжении только три возможности: 931, 842 и 964. (!)

19.13.Всю работу следует принять за единицу. Чтобы использовать условия задачи, нужно знать производительность одного комбайна. Однако нам неизвестно, сколько часов перед завершением работы по плану все комбайны работали вместе. Поскольку удобнее вводить одноименные неизвестные, то эту величину обозначим через y , а через x обозначим количество часов, необходимых одному комбайну, чтобы убрать весь урожай. Тогда производительность комбайна будет равна 1/ x .

19.14.Пусть братьям а , аq и аq ² лет. Если младший получит x рублей, то остальные два получат xq и xq ² рублей. Условия задачи позволяют составить три уравнения.

19.15.После того как числа, о которых говорится в задаче, будут обозначены буквами а , b и с и условия задачи будут переведены на математический язык, мы получим два уравнения с тремя неизвестными. Достаточно ли этого, чтобы решить задачу?

19.16.Воспользоваться методом математической индукции, что позволит доказать формулы для а n и b n .

19.17.Решив данное тригонометрическое уравнение, получим две серии углов, каждая из которых является арифметической прогрессией с известной разностью и первым членом, равным нулю. В каком случае две арифметические прогрессии могут быть объединены в одну?

20.1.Данное неравенство эквивалентно такому:

1/ 2² + ... + 1/ n ²< 1.

Оценить каждое слагаемое так, чтобы легко было оценить всю сумму, стоящую слева.

20.2.Домножить все члены на d .

20.3.Чтобы разложить дробь 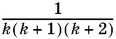на простейшие, можно начать с разложения дроби 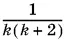, а результат умножить на .

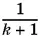20.4.Слева стоит сумма членов геометрической прогрессии.

20.5.Выписать все коэффициенты многочлена 1 + x + 2 x ² + ... + nx n и под ними написать коэффициенты того же многочлена, записанные в обратном порядке. Рассмотреть сумму произведений стоящих друг под другом чисел.