Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы
- Название:Сборник задач по математике с решениями для поступающих в вузы
- Автор:
- Жанр:
- Издательство:«ОНИКС 21 век» «Мир и Образование»
- Год:2003
- Город:Москва
- ISBN:5-329-00766-6, 5-94666-080-2
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы краткое содержание
Основу задачника составили варианты письменных работ по математике, предлагавшихся на вступительных экзаменах в ряде ведущих вузов Москвы.
Сборник содержит около 500 типовых задач. K каждой задаче дается до трех указаний, помогающих найти правильный путь к решению, а затем приводится подробное решение.
Пособие может использоваться при самостоятельной подготовке к экзаменам в вуз, а также на подготовительных отделениях и курсах.
Сборник задач по математике с решениями для поступающих в вузы - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
13.49.Воспользуйтесь тем, что 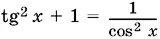 и cos З x + cos x = 2 cos 2 x cos x .
и cos З x + cos x = 2 cos 2 x cos x .
13.50.Разбить 4 ctg 2 x на слагаемые и в левой части образовать выражения 2(tg x + ctg 2 x ), tg x / 2+ ctg 2 x , ctg 2 x − ctg З х . Преобразовать каждое из этих выражений и затем преобразовать все уравнения к равной нулю дроби, у которой числитель и знаменатель — произведения тригонометрических функций.
13.51.Сделайте преобразование, имея в виду, что sin t ≠ 0, cos t ≠ 0, и воспользуйтесь соотношениями:
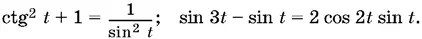
K главе 14
14.1.Если обе части неравенства возвести в квадрат, то получим равносильное неравенство. (!)
14.2.Использовать тот же прием, что и при решении уравнения cos x − sin x = −1, т. е. ввести вспомогательный угол. (!)
14.3. Способ 1.Можно перейти к неравенству относительно tg x . При этом придется рассмотреть различные случаи, в зависимости от знака cos x . (!)
Способ 2.Если синус и косинус выразить через tg x / 2, то получим квадратное неравенство. Равносильно ли оно данному? (!)
14.4.Если cos 2 x и sin 2 x выразить через tg x и обозначить tg x = y , то получится простое алгебраическое неравенство. Равносильно ли оно данному?
14.5. Способ 1.Можно перейти к совокупности двух систем: cos x и tg 2 x должны быть нестрого (т. е. включая нуль) разных знаков.
Способ 2.Воспользоваться формулой тангенса двойного угла. Равносильное ли получится неравенство?
14.6.Неравенство можно привести к алгебраическому, если выразить все тригонометрические функции через cos x . (!)
14.7.Если записать sin 2 x = 2 sin x cos x и перенести все члены неравенства в одну часть, то получим однородное выражение относительно sin x и cos x . Разделив на cos² x , получим алгебраическое неравенство относительно y = tg x . Равносильно ли оно данному? (!)
14.8.Вычислить дискриминант и выяснить, когда он положителен.
14.9.Неравенство может выполняться только при sin x ≥ 0 и cos x ≥ 0. Приняв во внимание эти ограничения, его можно возвести в квадрат. (!)
14.10.Записать решение неравенства в предположении, что 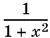 — новое неизвестное.
— новое неизвестное.
14.11.Привести к неравенству относительно одной тригонометрической функции.
14.12.Перенести −1 в левую часть, записать тангенсы через синусы и косинусы и выполнить сложение.
14.13.Это — иррациональное неравенство относительно у = cos x . Не следует забывать, что | у | ≤ 1. Благодаря этому решение можно упростить.
14.14.Если выразить sin x и cos x через tg x / 2, то получим алгебраическое неравенство, которое решается методом интервалов. (!)
14.15.Выразить все тригонометрические функции через sin α.
14.16.Так как sin² x ≥ 0, то, заметив, что x = π k — решения неравенства, можно изолировать параметр а ², разделив обе части неравенства на sin² x .
14.17.Если обозначить cos t = z , то данное выражение запишется в виде квадратного трехчлена относительно z , который должен быть положительным при всех −1 ≤ z ≤ 1. Найдите абсциссу вершины соответствующей ему параболы.
K главе 15
15.1.В правой части можно произвести логарифмирование, не нарушая равносильности.
15.2.Рассмотреть случаи 0 < tg x < 1 и tg x > 1. Удобно выразить sin² x через tg² x . (!)
15.3.Нетрудно заметить, что на самом деле интервал можно сузить: 0 < x < π/ 2, так как при π/ 2< x < π функции, стоящие под знаком логарифма, отрицательны.
15.4.Вначале нужно привести все логарифмы к общему основанию с помощью формулы log a kN = 1/ k log aN .
15.5.Неравенство эквивалентно условию, что основание логарифмов лежит между 0 и 1.
15.6.Начать следует с приведения левой части к виду, удобному для логарифмирования. Это позволит перейти к неравенствам, где уже не будут участвовать тригонометрические функции.
15.7.Использовать тот факт, что arccos у ≥ 0. Чему равносильно данное в условии неравенство?
15.8.Область значений левой части неравенства — интервал от 0 до π/ 2, а область значений правой части — интервал от 0 до π. Так как левая часть должна быть больше правой, то аргумент арккосинуса не может стать отрицательным.
15.9.Второй сомножитель неотрицателен при всех x , следовательно, неравенство может удовлетворяться лишь при положительных значениях первого сомножителя. Если произведение двух положительных чисел не меньше единицы, то хотя бы одно из них не меньше единицы.
15.10. Обозначим первый сомножитель через А , а второй через В . Так как А ≥ 0, то неравенство равносильно совокупности двух систем:
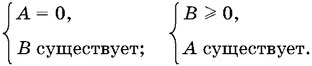
K главе 16
16.1.Правая часть уравнения не может стать меньше двух. Сравнить с оценкой левой части. (!)
16.2.Это уравнение легко привести к квадратному относительно 2 tg² x . (!)
16.3.Перейти к общему основанию. Не нарушится ли при этом равносильность?
16.4.Поскольку в левой части уравнения стоит произведение синуса и косинуса от одного аргумента, удобно воспользоваться формулой синуса двойного угла. Записать, чему равен аргумент.
16.5.Перейти к уравнению без логарифмов, позаботившись о сохранении ограничений.
16.6.Ввести вспомогательное неизвестное и преобразовать данное уравнение в квадратное. (!)
16.7.От этого уравнения легко перейти к тригонометрическому. При этом нужно учесть все ограничения, которыми логарифм связывает число и основание.
16.8.Уравнение равносильно уравнению 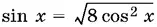 при условии, что cos² x ≠ 1/ 8.
при условии, что cos² x ≠ 1/ 8.
16.9.Перейти к уравнению 5π(½) x = π/ 4+ π k и найти все k , при которых это равенство возможно.
16.10.Вначале решить квадратное уравнение относительно lg cos x . Затем найти cos x и на этом шаге провести исследование.
16.11.Решить квадратное уравнение и учесть все ограничения на параметр а в связи с появлением радикала и синуса.
Читать дальшеИнтервал:
Закладка:










