Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

20.6.В левой части неравенства стоит абсолютная величина суммы членов бесконечной геометрической прогрессии со знаменателем −2 x .

20.7.Каждое слагаемое k · k ! можно представить в виде ( k + 1) k ! − k ( k − 1)!. При этом следует иметь в виду, что 0! = 1. (!)

20.8.Коэффициенты в правой части образуют арифметическую прогрессию с разностью 3. Если домножить S n на x ², то справа получим сумму, все члены которой, кроме крайних, имеют коэффициент, отличающийся от подобного коэффициента S n на 3.

20.9.Рассмотреть тождество

( x + 1) 5= x 5+ 5 x 4+ 10 x ³ + 10 x ² + 5 x + 1

и положить в нем последовательно x = 1, 2, ..., n .

20.10.В n -й группе n членов. Рассмотрите отдельно случаи, когда n четное и n нечетное.

20.11.Удобнее найти 2 S n sin π/ 2 n .

20.12.Можно разбить эту сумму на 1 00 сумм:

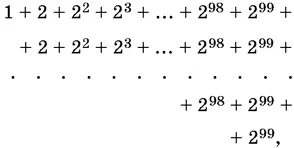
каждая из которых является суммой членов геометрической прогрессии. Однако попытайтесь решить эту задачу проще, обозначив искомую сумму через в и осуществив над ней некоторое несложное преобразование.

20.13.Общий член ряда имеет вид 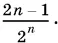Чтобы воспользоваться формулой геометрической прогрессии, нужно избавиться от 2 n в числителе. Чтобы понять, как это лучше сделать, запишите рядом два соседних члена ряда.

21.1.Если все, сидящие за круглым столом, одновременно сдвинуться на один стул в одном направлении, то у каждого останутся те же самые соседи.

21.2.Представить искомое число в виде разности числа всех перестановок из пяти элементов и перестановок, не удовлетворяющих условиям задачи.

21.3.Три разряда каждого числа должны быть заняты двойками. В оставшиеся четыре разряда можно поместить любые из восьми цифр, что даст 8 4вариантов.

21.4.Задачу следует начать решать в предположении, что есть разные цифры l 1, l 2 и l 3, которые входят в каждое число, а остальные пять цифр равноправны.

21.5.Легче найти число всевозможных размещений экскурсантов по каютам в предположении, что каюты неравноценны. Пусть таких размещений будет N , а размещений, о которых идет речь в задаче, K . Поскольку из каждого размещения экскурсантов по равноценным каютам можно получить 8! размещений по неравноценным каютам, то K · 8! = N .

21.6.В записи k -го члена суммы произвести сокращение на k .

21.7.Нужно найти такие n , для которых равенство

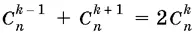
выполняется при некотором k .

21.8.Представить а + b + с + d в виде ( а + b ) + ( с + d ) и осуществить возведение в n -ю степень по правилам возведения в степень двучлена.

21.9.Коэффициент при x k будет равен числу членов, содержащих x k при почленном перемножении двух одинаковых многочленов. Придется различать случай, когда члены, содержащие x k , могут быть получены в результате умножения друг на друга членов суммы 1 + x + x ² + ... + x k − 1+ x k (0 ≤ k ≤ n − 1), от случая, когда n − 1 < k ≤ 2( n −1).

21.10.Записать выражение для общего члена разложения и сравнить с выражением для десятого члена разложения.

21.11.Сгруппировать члены внутри скобки и последовательно дважды применить формулу бинома.

21.12.Если обозначить через Р n число способов, которыми можно разбить на группы последовательность из n элементов, то можно получить рекуррентную формулу для Р n .

21.13.Если на плоскости проведены m параллельных прямых, то они разбивают плоскость на m + 1 частей. Когда мы пересечем их некоторой прямой, то каждая часть разобьется на две. Что произойдет, если к уже проведенным k непараллельным прямым добавить еще одну?

22.1.Перенести acrtg 7/ 23в правую часть, после чего оценить значения обеих частей с тем, чтобы они попали в интервал (0, π/ 2). (!)

22.2.Каждое из двух первых слагаемых лежит в интервале (0, π/ 4). Это позволяет воспользоваться формулой тангенса суммы и заменить два первых слагаемых одним.

22.3.Начать нужно с представления в виде значения одной тригонометрической функции первого и третьего слагаемых. Чтобы их сумма попала в область главных значений арккотангенса, придется прибавить к ней π. (!)

22.4.Если 0 ≤ x ≤ 1, то сумма существует и лежит в интервале [0, π], т. е. в интервале монотонности косинуса.

22.5.Начать нужно с выяснения, в каком интервале лежит π( x ² + x − 3), если 0 ≤ x ≤ √3 − 1/ 2.

22.6.Убедившись в существовании арксинусов при 0 ≤ x ≤ 1, перенести π/ 4в левую часть, а вычитаемое — в правую, затем доказать, что левая часть равенства будет лежать в интервале монотонности синуса. (!)

22.7.Так как x < −1, то значение каждой функции, входящей в правую часть, можно уточнить с тем, чтобы сумма попала в интервал монотонности синуса и тангенса. (!)

22.8.Из данного уравнения можно найти значения arcsin x . Из этих значений остается выбрать те, которые лежат в области значений арксинуса. (!)

22.9.Поскольку arcsin x — нечетная функция, то одновременно с корнем x уравнение имеет корень − x . Это позволяет искать лишь неотрицательные корни.

22.10.Из условия следует, что x > 0. Левая часть заключена в интервале [0, π], который является интервалом монотонности косинуса.

22.11.Воспользовавшись тем, что 2 + cos x > 0 и 2 cos² x / 2 ≥ 0, можно уточнить интервал значений левой части уравнения.

22.12.Левая и правая части лежат в интервале монотонности синуса. (!)

22.13.Уточнение интервалов с тем, чтобы получить равносильное уравнение, приведет к нерациональному способу решения. Проще перенести, например, arctg ( x + 1) в правую часть и взять котангенсы от обеих частей. Каким образом может быть нарушена равносильность?

23.1.Поскольку sin x ≤ 1, то log 3sin x ≤ 0. (!)

23.2.В указанной последовательности действий первое ограничение накладывается на трехчлен x ² − x − 1, он должен быть положительным. Следующее ограничение накладывается уже на log ½( x ² − x − 1). (!)

23.3.Нужно пройти всю последовательность действий, начиная с самого внутреннего, и записать все встречающиеся при этом ограничения. (!)