Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

2.8.В треугольнике А 1 АА 2известны основание и высота. Третий элемент этого треугольника можно найти, если использовать данный в условии угол А треугольника АВС , через который легко выразить угол А 1 АА 2.

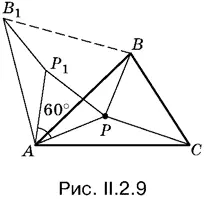
2.9.Если взять любой из треугольников, образовавшихся при вершине P (рис. 11.2.9), то начало для построения ломаной, составленной из АР , ВР и СР , уже есть. Однако просто пристроить недостающее звено нельзя, так как последняя вершина такой ломаной не будет закреплена, а потому не позволит решить задачу.

На помощь приходит свойство правильного треугольника: поверните треугольник АВР на 60° вокруг точки А и вы получите ломаную В 1 Р 1 РС , равную сумме отрезков АР , ВР и СР . При этом точка В 1однозначно определяется видом треугольника АВС .

2.10.Чтобы построить точку С , достаточно знать длину отрезка СЕ или длину отрезка DЕ = СЕ − l . Задача сводится к вычислению и построению отрезка DЕ .

2.11.Вершина С лежит, с одной стороны, на окружности радиусом b с центром в точке В , а с другой стороны, на прямой, параллельной АD , которую нетрудно построить.

2.12.Остается построить треугольник ОМС по трем сторонам: СМ = АО = R , ОС = 2 R , ОМ известно, так как точки О и M даны.

2.13.Треугольник ОО 1 E , где О 1 E ‖ AB , а точка E лежит на ОС , легко построить, зная О 1 Е = a / 2.

2.14.Точки M и N лежат на окружности, концентрической данной.

2.15.Отрезок РQ перенести параллельно в отрезок В 1 В и рассмотреть угол АРВ 1.

2.16.Чтобы построить параллелограмм FBDE на его диагонали, нужно найти еще одну связь между вершинами F и D и данными элементами. Заметим, что точка А еще никак не участвовала в построениях. Если соединить ее с точкой F то получим угол АFЕ , который известен, так как выражается через угол АСВ .

2.18.Воспользоваться тем, что высоты в треугольнике пересекаются в одной точке.

2.19.Провести прямую через точку С и данную точку M и найти точку ее пересечения с данным диаметром или его продолжением.

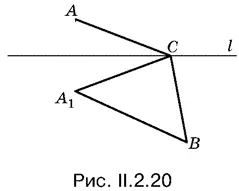
2.20.Если одну из точек, например А , отразим симметрично от прямой l (рис. II.2.20), то получим точку А 1причем решение аналогичной задачи для точек A 1и В совпадет с решением первоначальной задачи. Легко заметить, что величина | A 1 C − BC | не может превзойти длины отрезка A 1 B . Но может ли она ее достигнуть?

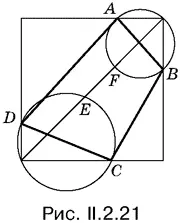
2.21.Такая связь есть (рис. II.2.21). Точки E и F пересечения диагонали квадрата с окружностями, построенными на противоположных сторонах данного четырехугольника как на диаметрах, делят соответствующие дуги пополам.

2.22.Выбрав произвольно длину отрезка 1, построим соответствующий ему отрезок длины √7. Теперь, зная отрезки 1 и √7, найдем отрезок x = 7, воспользовавшись подобием соответствующих треугольников: √7 : x = 1 : √7 .

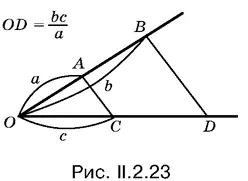
2.23.Если на одном луче от вершины О угла отложены отрезки ОА = а и ОВ = b ( b > а ), на другом его луче отрезок ОС = с (рис. II.2.23), и через точку В проведена прямая BD , параллельная AC и пересекающая ОС в точке D , то отрезок OD = d = bc / а .

3.1.Выразить длину отрезка ОС через ОА .

3.2.Данный треугольник и все треугольники, образовавшиеся при его проецировании на плоскость P , определены с точностью до подобия. Поэтому соотношение между углами можно получить, введя в рассмотрение некоторый линейный элемент, зависящий от всех участвующих в задаче углов. (!!)

В качестве линейного элемента взять расстояние от вершины прямого угла треугольника до плоскости P .

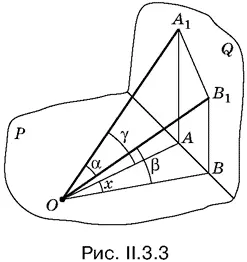
3.3.При построении плоскости Q мы можем произвольно выбрать две величины: расстояние от точки О до этой плоскости и угол АВО (рис. II.3.3), чтобы пирамида ОАА 1 В 1 В имела наиболее удобный вид. При изменении расстояния от точки О до плоскости Q возникает фигура, подобная первоначальной. Это не отражается на рассматриваемых углах, а потому позволяет ввести линейный элемент, через который мы выразим затем все стороны треугольника ОАВ . (!!)

В качестве линейных элементов удобно выбрать отрезки AA 1или ВВ 1так как это позволяет легко вычислить стороны треугольника ОАВ и затем угол АОВ . Однако мы должны выбрать лишь один линейный элемент. Поэтому расположим плоскость Q так, чтобы AA 1= ВВ 1.

3.4.Точка, в которую спроецируется искомая прямая, должна быть одинаково удалена от проекций прямых b , с и d . Рассмотреть различные случаи расположения проекций, которые могут возникнуть.

3.5.Чтобы связать искомый угол с треугольником и отрезком AS , построим в плоскости P прямоугольник, две стороны которого лежат на AB и CD , а AC — его диагональ.

3.6.Отрезок OK можно выразить из треугольников OKM и OKR и приравнять полученные выражения. Еще одно соотношение между интересующими нас величинами получим с помощью отрезка АР . Останется воспользоваться равенством, содержащимся в условии.

3.7.В двух противоположных гранях четырехгранного угла должны лежать параллельные стороны параллелограмма. Однако эти грани имеют общую точку — вершину угла, поэтому они пересекаются по некоторой прямой. Противоположные стороны параллелограмма должны быть параллельны этой прямой.

3.8.Рассмотреть треугольник FBA и убедиться, что угол CAF прямой.

3.9.Если вершина пирамиды спроецируется в точку, лежащую внутри основания, то с помощью сравнения площадей легко сосчитать, чему равна сумма расстояний от этой точки до сторон треугольника. (!!)

Расстояния от точки, в которую проецируется вершина пирамиды, до сторон треугольника выражаются через высоту пирамиды и данные углы. Пользуясь этим, можно вычислить высоту пирамиды. Случай, когда вершина проецируется не внутрь основания, не доставляет ничего нового.