Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

3.10.Высота DO пирамиды будет лежать в плоскости EDC (докажите). Ее можно выразить сначала через ED , а затем через ЕС и искомый угол.

3.11.Чтобы вычислить площадь боковой поверхности пирамиды, нужно найти либо боковое ребро, либо тригонометрические функции угла x . Второе сделать легче, так как углы x и 2 x встречаются в двух различных прямоугольных треугольниках с одинаковой гипотенузой.

3.12.Начать нужно с определения коэффициента пропорциональности длин параллельных ребер тетраэдров. Для этого придется рассмотреть треугольник, образованный двумя медианами, которые принадлежат разным треугольникам, но опираются на одно ребро тетраэдра.

3.13.Чтобы установить равенство треугольников A 1 SB 1и A 2 SB 3, достаточно доказать, что равны их углы при вершине S . Мы не использовали еще полностью то условие задачи, в силу которого О — центр шара, вписанного в трехгранный угол. Поэтому целесообразно рассмотреть плоскость, проходящую через ОО 1и ОО 2и точку ее пересечения с SA 2.

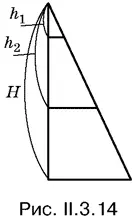
3.14.Достаточно ограничиться рассмотрением схематического рис. II.3.14, имея в виду, что H − h 2= H − h 1/ 2. Это соотношение соответствует условию, согласно которому интересующее нас сечение проходит через середину высоты усеченной пирамиды.

3.15.Если вычислить DE ², то косинус угла DAE найдем с помощью теоремы косинусов из треугольника ADE . Вычислить DE ² можно, воспользовавшись тем, что DO — медиана одновременно в двух треугольниках: ADC и BDE .

3.16.Углы α и β в сумме образуют угол, все тригонометрические функции которого известны. Взяв, например, cos (α + β), мы получим еще одно уравнение.

3.17.Треугольники DAM и DMS имеют общую сторону MD и смежные углы при вершине M . Следовательно, отношение их площадей равно отношению отрезков AM и MS . Воспользоваться подобием треугольников, образовавшихся в плоскости ASB . (!!)

Ввести линейный элемент, через который выразить длины отрезков. Удобно выбрать сторону квадрата, лежащего в основании, так как равный ей отрезок KE связывает с помощью углов α и β все элементы в треугольнике KSE .

3.18.В треугольниках ADC и ADB углы при вершине D прямые.

3.19.Плоскостью SDC пирамида SABC разбилась на две равные пирамиды с общим основанием SDC . Для решения задачи нужно найти площадь SDC , так как высоты пирамид известны.

3.20.Чтобы связать участвующие в задаче элементы, нужно измерить данный двугранный угол α и искомый двугранный угол x . Высота пирамиды свяжет эти два угла.

3.21.Рассмотрите треугольник ABD , стороны которого легко выразить через SA и тригонометрические функции угла α. (!!)

Из треугольника ABD найдите косинус угла x .

3.22.Отрезок KM можно, во-первых, вычислить непосредственно, а во-вторых, выразить через R .

3.23.Построенное сечение пересечет основание пирамиды по отрезку, параллельному одному из ребер основания. (!!)

Воспользоваться сравнением площадей для треугольника SOA .

3.24.На рис. I.3.24 (см. с. 127) спроецируйте DС на плоскость основания. Докажите утверждение, обратное сформулированному в первом указании: если проведена плоскость KLNM , параллельная AB и DC , то KLNM — прямоугольник. Выясните, когда он будет квадратом, воспользовавшись подобием образовавшихся на рисунке треугольников.

3.25.Из точки R 1на три грани пирамиды опущены перпендикуляры одинаковой длины. Если соединить точку R 1со всеми вершинами пирамиды, то этот факт можно будет использовать при сравнении объемов.

3.26.Чтобы найти площадь основания пирамиды, нужно сначала выразить площадь сечения А 1 В 1 С 1(см. рис. I.3.26 на с. 127) через ребро куба, а затем воспользоваться соотношением между площадями подобных фигур.

3.27.С помощью боковых ребер x , y , z пирамиды можно записать выражение для ее объема V = xyz / 6. Остается выразить x , y и z через a , b и с .

3.28.Если EF — проекция DC на плоскость P , то АЕВF — прямоугольник (докажите). (!!)

Плоскость DCFE разобьет пирамиду АВСD на две равные пирамиды с общим основанием, площадь которого легко вычислить, и высотой, которую можно найти из прямоугольника AFBE .

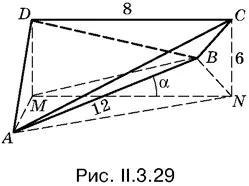
3.29.Если вы правильно воспользовались первым указанием, то получите рис. II.3.29.

Пусть MN — проекция CD на плоскость P . Тогда СN = DM = 6, MN и AB образуют искомый угол α. Применение метода сравнения объемов для тела АNВMСD позволяет получить уравнение относительно sin α.

3.30.Если ввести в рассмотрение высоту H призмы и сторону a ее основания, то из правильного треугольника В 1 А 1 С 1мы легко выразим a через R , а с помощью треугольника DА 1 Е выразим и H через R . (!!)

Для треугольника DА 1 E применить метод сравнения площадей.

3.31.Рассмотреть треугольник, образованный высотой тетраэдра, одним из боковых ребер и проекцией этого ребра на плоскость основания, а также подобный ему треугольник, в котором участвует искомый радиус.

3.32.Из всех подобных кубов с центром в точке О удобно выбрать тот, вершина которого, противоположная точке О , лежит на грани параллелепипеда.

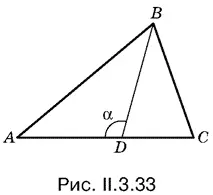
3.33.Пусть разность между углами А и С равна φ, а ВD — биссектриса угла В (рис. II.3.33). Легко показать, что α = π/ 2+ φ/ 2. Затем удобно представить площадь треугольника АВС как сумму площадей треугольников АDВ и ВDС .

3.34.Расстояние между диагоналями С 1 D и В 1 С (рисунок сделайте сами) равно расстоянию между плоскостями А 1 C 1 D и АВ 1 С .

3.35.Основание перпендикуляра, опущенного из точки K на диагональ куба, обозначим через О 1. Для треугольника OKO 1можно воспользоваться свойством отрезков, на которые биссектриса делит сторону основания.

3.36.Перемещая взаимно перпендикулярные плоскости параллельно самим себе, мы не изменим проекции четырехугольника. Поэтому разместим одну из плоскостей так, чтобы она проходила через вершину четырехугольника (рис. II.3.36; эта вершина обозначена буквой А). Чтобы построить прямую, по которой пересекаются плоскости АВСD и АВ 1 С 1 D 1, найдем точку E , в которой пересекаются BC и В 1 С 1. Теперь можно измерить угол между плоскостями АВСD и АВ 1 С 1 D 1, построив ВF ⊥ ЕА и соединив В 1с F . Угол ВFВ 1равен 45°.