Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

5.5.Если прямые AB и CD пересекаются в точке N , то отрезки AB и CD следует перенести в эту точку, двигая каждый по своей прямой. После этого задача сведется к предыдущей (см. задачу 5.4). (!!)

Если прямые AB и CD параллельны, то отрезки AB и CD удобно расположить так, чтобы их центры лежали на общем перпендикуляре. Этот перпендикуляр остается разделить в отношении CD : AB .

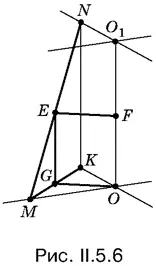
5.6.Пусть MN — отрезок длины l , E — его середина, а длина отрезка ОО 1равна а (рис. II.5.6). Если спроецировать точку E на плоскость нижнего основания, то легко вычислить длину отрезка GO , равного отрезку EF . (!!)

Поскольку длина отрезка GO , равного отрезку EF , не зависит от расположения отрезка MN , то точка E лежит на окружности радиуса EF с центром в точке F . Остается установить обратное предположение и вспомнить о том, что отрезок не должен находиться вне куба.

6.1.Воспользоваться тем, что p − 1, p , p + 1 — три последовательных числа, причем p — простое, большее трех.

6.3.Если n = 2 k + 1, то а n + b n = ( а + b )( а n − 1− ... + b n − 1).

6.4.Среди этих же чисел будет 125/ 2= 62 [16] [ x ] — целая часть числа x . , делящихся на 8 = 2³ и т. д.

6.5.Так как сумма цифр числа делится на 81, то естественно предположить, что оно делится на 81. Однако такой признак делимости не был доказан в курсе арифметики, и поэтому придется дважды воспользоваться признаком делимости на 9. Для этого удобно разбить цифры числа на 9 групп, каждая из которых делится на 9.

6.6.Если многочлен n 4+ 4 разложен на множители второй степени, то он может быть простым числом только в том случае, если один из множителей равен единице.

6.7.Чтобы убедиться, что числитель всегда делится на число, стоящее в знаменателе, его придется разложить на множители.

6.8. Способ 1.Предположим, что данная дробь сократима. Тогда 5 x + 7 = qr , 2 x + 3 = pr . Рассматривая эти равенства как систему уравнений относительно x , исключим x .

Способ 2.Рассмотреть вместо данной дроби обратную и выделить целую часть.

6.10.Пример дальнейших рассуждений: при умножении цифры с на 3 мы должны получить число, оканчивающееся на 1. Это возможно лишь при с = 7.

6.11.Так как p — число нечетное, то мы имеем три последовательно нечетных числа. Докажите, что одно из них обязательно делится на 3.

6.12.Если tg 5° — рациональное число, то cos 10° и cos 30° — тоже рациональные числа.

6.13.Сумма девяток должна быть на 10, или на 21, или на 32, или на 43, ... меньше числа, которое делится на 11. Чему должны быть равны в сумме остальные цифры?

6.14.Однородные выражения удобно преобразовывать с помощью замены у = kx . Так как x и у — целые числа, то число k — рациональное, т. е. k = p / q . Остается рассмотреть возможные значения сомножителей, произведение которых равно 17. Нужно добиться того, чтобы каждый сомножитель был целым числом.

6.15.Удобно записать уравнение в виде ( x − 2 у )( x + 2 у ) = 5² · 9 · 89 и вспомнить, что мы ищем целочисленные решения.

6.16.Условие 11(4 x − 1) = 69( у − x ) удовлетворяется при целочисленных значениях x и у , только если 4 x − 1 = 69 k , у − x = 11 n . Из первого соотношения следует, что k + 1 делится на 4. Отсюда k = 3, 7, 11, ... .

7.1.Вынести за скобки в числителе 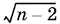, а в знаменателе 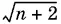. После этого дробь сократится.

7.2.Трехчлен 1 + x − x ² является общим множителем знаменателей дробей в первой скобке.

7.3.Последнее слагаемое нужно преобразовать отдельно, после чего его можно будет объединить с первыми двумя.

7.4.Поскольку степень каждого члена числителя вдвое больше степени соответствующего члена знаменателя, то дробь целесообразно умножить на выражение, сопряженное знаменателю.

7.6.Преобразовать подкоренные выражения, прибавив и вычтя из них единицу. При извлечении корня использовать условия задачи.

7.7.Можно воспользоваться формулой сложного радикала

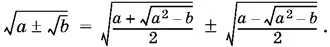
7.9.Возвести левую часть, равную 2, в куб, воспользовавшись формулой ( x + у )³ = x ³ + у ³ + 3 xу ( x + у ), где x + у = 2.

7.10.Равенство а + b = − с возвести в куб, а равенство а + b + с = 0 дважды возвести в квадрат. Полученные таким образом соотношения учесть при преобразовании левой части равенства, которое нужно доказать.

7.11.Итак, можно безболезненно рассмотреть лишь случай x ≥ 0, у — любое. Его придется разбить на два случая: | у | ≤ x и | у | > x . В последнем случае .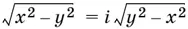

7.12.Возведенное в куб выражение преобразовать и упростить, воспользовавшись им же.

7.13.Тождественное равенство многочленов означает равенство их коэффициентов:

а ³ − с ³ = 0, 3( а ² b − с ²) = 24, ... .

Из первого равенства следует, что а = с , после чего можно упростить все другие соотношения.

8.2.Перемножить первую скобку с третьей, а вторую с четвертой.

8.5.Полученное тождество справедливо при всех значениях x , в частности при x = i .

8.6.Полезно заметить, что при целых значениях x ≠ 0 выражение 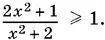Это позволяет ограничиться рассмотрением таких целых у , что у ² ≤ 6.

8.7.Так как все коэффициенты уравнения — рациональные числа, то можно предвидеть, что наряду с корнем √3 + 1 должен существовать корень √3 − 1.

8.8.Теоремы Виета недостаточно, так как уравнение в этом случае может вовсе не иметь действительных корней.

8.11.Приравнять остаток нулю и потребовать, чтобы квадратный трехчлен, получившийся в частном, был положителен, т. е. имел отрицательный дискриминант.

8.12.В полученном тождестве следует выбрать x = 2 и x = 3. Получим два уравнения относительно а и b .