Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

В плоскости Π образуется пятиугольник специального вида. Такой пятиугольник можно получить, если на одно из оснований прямоугольника поставить равнобедренный треугольник.

3.51. Способ 1.Из полученного тригонометрического уравнения удобно определить cos 2α и воспользоваться этой величиной для нахождения отношения V к: V ш.

Способ 2.Естественно воспользоваться леммой, в силу которой V 1= ⅓ rS 6, т. е. объем первого тела вращения равен одной трети произведения радиуса вписанного в конус шара на его боковую поверхность.

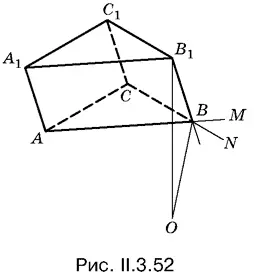
3.52.Вершина В 1может проецироваться на биссектрису угла ABN (или угла СВМ ) — внешнего угла треугольника АВС (рис. II.3.52). Поэтому придется рассмотреть два различных случая, каждому из которых соответствует свой рисунок.

3.53.Разделите куб АВСDА 1 В 1 С 1 D 1на две равные призмы плоскостью, проходящей через ребра В 1 С 1и АD . Каждую из двух призм разделите на две пирамиды, одна из которых — четырехугольная, а другая — треугольная.

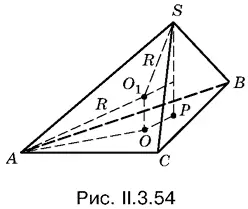
3.54.Центр описанного около пирамиды SABC шара обозначим через O 1. Он лежит на перпендикуляре ОО 1к плоскости АВС , проведенном через центр О правильного треугольника АВС (рис. II.3.54). Возникает соблазн сделать вывод о том, что радиус описанного шара достигает минимального значения, когда вершина S совпадает с центром Q треугольника А 1 В 1 С 1. В этом случае радиус O 1 S = O 1 Q становится частью перпендикуляра, в то время как в остальных случаях O 1 S — наклонная и поэтому меньше своего перпендикуляра. K сожалению, это рассуждение некорректно, так как при изменении положения вершины S , вообще говоря, меняется положение центра шара О 1, хотя он и остается на прямой ОО 1. (!!)

Есть еще одна тонкость. Мы не можем заранее утверждать, что центр шара О 1лежит между точками О и Q . Вполне может случиться, что точка О ближе к точке Q , чем точка О 1. Решение должно учитывать и это обстоятельство.

4.1.Если ребро куба обозначить через а , то объем фигуры, лежащей под сечением, можно вычислить как разность объемов двух треугольных пирамид: NАFD и МЕFС (рис. I.4.1 на с. 131).

4.2.Площадь сечения удобно вычислять как разность между площадью треугольника AML (см. рис. I.4.2 на с. 131) и удвоенной площадью треугольника KGL .

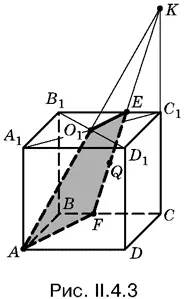
4.3.Построение сечения показано на рис. II.4.3. Обратите внимание на то обстоятельство, что EС 1= BF .

4.4.Объемы пирамид, о которых шла речь в конце указания I (см. с. 132), нужно выразить через объем данной пирамиды SABCD . Для этого придется найти отношение их высот и оснований. Сделайте отдельный чертеж плоскости, в которой лежит грань SDC .

4.5.Чтобы сравнить объемы фигур, на которые разбивается сечением вторая половина данной пирамиды, удобно в качестве основания выбрать грань BSC .

4.6.Если продолжить ребра А 1 D 1и А 1 B 1до пересечения с QR и QP соответственно, то можно будет построить след сечения в плоскости верхнего основания куба.

4.7.Обозначить сторону основания через а и выразить площадь сечения через а и высоту боковой грани.

4.8.Нужно доказать, что точка D лежит на отрезке KM (см. рис. I.4.8 на с. 132). Однако сделать это непосредственно трудно. Удобнее изменить построение: EK — высота пирамиды ЕАВС , D — середина AC . Проведем через K и D прямую, которая пересечет AB в точке M . Докажем, что ЕМ — высота в треугольнике АВЕ . (!!)

Если мы убедимся в том, что KSOD — параллелограмм, то отрезок KD параллелен СО и, следовательно, перпендикулярен к AB , откуда ЕМ — высота треугольника АВЕ .

4.9.В сечении получается пятиугольник, в котором отрезок, параллельный АС 1, не является высотой, так как основания параллелепипеда — не квадраты. Высоту нужно вычислить, чтобы найти площадь пятиугольника.

4.10.Докажите, что при вращении точки E тень, отбрасываемая верхним основанием куба, перемещается, оставаясь квадратом со стороной 2 h . (!!)

Тень при любом положении источника E состоит из двух квадратов АВСD и А 2 В 2 С 2 D 2, стороны которых параллельны, сторона второго вдвое больше стороны первого, а отрезок, соединяющий центры, имеет постоянную длину R . Чтобы построить из этих квадратов тень, нужно соединить соответствующие вершины квадратов и получить выпуклую фигуру. Задача свелась к плоской.

4.11.Если вместо куба, нижнее основание которого образует с плоскостью Π острый угол φ, оставить фигуру А 1 В 1 D 1 DВС , образованную двумя треугольниками A 1 B 1 D 1, ВСD и диагональным сечением В 1 D 1 DB куба, то отбрасываемая на плоскость Π тень не изменится. Остается выразить площадь тени через ребро куба и угол φ.

5.2.В треугольнике АМВ рассмотреть медиану, выразить ее квадрат через стороны треугольника, воспользоваться полученными ранее соотношениями. (!!)

Доказать, что медиана МС равна AB .

5.3.Косинус угла А , участвующий в теореме косинусов, можно определить из треугольника АМО , где О — центр окружности, о которой идет речь в условии задачи. (!!)

Обратное утверждение можно доказывать в такой форме: если AC = 2 ВС и 2 АМ ² + МВ ² = АВ ², то АО = МО . Здесь тоже естественно воспользоваться теоремой косинусов для треугольника АМВ . Единственное осложнение возникает из-за необходимости выразить cos А через линейные элементы. Можно поступить иначе: записать теорему косинусов для треугольника АМО , имеющего с АМВ общий угол А , и исключить cos А .

5.4.Два треугольника АМВ и ВМС , имеющие общую сторону ВМ , равновелики тогда и только тогда, если их высоты, опущенные из вершин А и С на общую сторону ВМ , равны.

Задача свелась к построению прямой, проходящей через точку В и равноудаленной от двух данных точек А и С . (!!)

Существуют две и только две прямые, проходящие через точку В и равноудаленные от точек А и С : одна — параллельная AC , другая проходит через середину AC .