Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

Придется рассмотреть существование решений первого неравенства при u > 1 для разных случаев относительно коэффициента при u ² функции f ( u ), т. е. v ² − 1 > 0; v ² − 1 = 0; v ² − 1 < 0.

17.10.Если а — целое, то дискриминант данного уравнения есть квадрат целого числа, т. е. а ² − 2 а − 19 = n ². Отсюда ( а − 1)² − n ² = 20. Левую часть нужно представить в виде произведения целых чисел.

17.11.Случаи, когда y = 0 нужно рассмотреть отдельно. Определить соответствующие а и для каждого из них решить исходное уравнение. До этого выводов о числе корней исходного уравнения делать не следует.

17.12.Исходное уравнение при y = sin 4 x преобразуется к виду

( а + 3) y ² + (2 а − 1) y + ( а − 2) = 0,

где | y | ≤ 1.

Исследуйте отдельно случаи D = 0 и D > 0, для каждого из которых найдите значения а , удовлетворяющие условию, в силу которого равно восемь решений исходного уравнения (см. условие задачи) попадают на отрезок [−π, π]. (!!)

При замене переменной z = 4 x получаем уравнение

( а + 3) sin² z + (2 а − 1) sin z + (а − 2) = 0,

или

( а + 3) y 2+ (2 а − 1) y + ( а − 2) = 0,

где y = sin z ; | y | ≤ 1.

Если существует решение второго уравнения y 1 ∈ (−1, 1), т. е. y 1лежит внутри интервала (−1, 1), то этому y 1соответствуют ровно два значения z ∈ (−π, π) и ровно восемь значений x ∈ (−π, π). (Для z период синуса равен 2π, а для x = z / 4период синуса уменьшится в 4 раза и будет равен π/ 2, т. е. внутри каждого интервала длиной π/ 2мы получим два решения для x , а внутри интервала (−π, π) таких решений будет восемь.)

17.13.Если ( x , y ) — фиксированная точка плоскости и через эту точку проходит кривая семейства, то должно существовать, по крайней мере одно соответствующее ей значение параметра а . Рассмотрев уравнение семейства кривых как уравнение относительно а, мы и получим соответствующие ограничения.

18.1.Этих трех уравнений достаточно; чтобы ответить на вопрос задачи, нужно из первого уравнения вычесть поочередно второе и третье.

18.2.Найти минимум P .

18.3.Так как числа 20, 21 и 23 очень близки, то дальше удобно рассуждать, предполагая, что все 500 марок расклеены по 20 на один лист — тогда двух альбомов заведомо не хватит, и по 23 на один лист — тогда в двух альбомах останется не менее одного пустого листа.

18.4.Легко доказать, что x = y . B самом деле, первый и второй понтоны прошли весь путь за равное время, т. е.

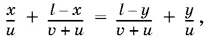
откуда

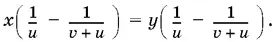
Так как v ≠ 0 и u ≠ 0, то x = y .

18.5.При решении уравнений нужно помнить, что x и y — цифры, а потому число их возможных вариаций ограничено.

18.6.Цена второй части бриллианта l ( p − x )². Остается сравнить цену двух частей с ценой целого бриллианта.

18.7.Удобнее ввести в рассмотрение нормы расхода горючего, отнесенные к часу работы двигателя, так как нормы расхода на километр пути в стоячей воде пришлось бы пересчитывать на нормы для движения против течения.

18.8.Решать систему уравнений нужно методом исключения. При этом последнее уравнение будет содержать два неизвестных, одним из которых должно быть s . Использовать условие y > s и решить это уравнение в натуральных числах.

18.9.Путь отрезок AC вниз по течению пароход проходит за (40 − x / 2) ч, а тот же путь вверх по течению — за (48 − x / 2) ч. Это позволяет найти скорость течения.

18.10.B качестве неизвестных удобно выбрать скорости пловцов и расстояние AC .

18.11.Если раствор занимал первоначально x -ю часть сосуда, то чистой кислоты в нем было xp / 100, а долили (1 − x ) q / 100чистой кислоты. Концентрация полученного таким образом раствора равна

p 1= px + (1 − x ) q .

Мы получили рекуррентную формулу для р k — концентрации после k циклов. Остается выразить р k через p .

18.12.Чтобы вычислить расстояние между пунктами первой и второй встречи, нужно сначала определить время между этими двумя встречами, т. е. разделить длину отрезка между пунктом первой встречи и пунктом B на сумму скоростей. Полученное выражение нужно умножить на скорость автомобиля. B результате получим уравнение

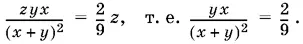
Два уравнения, в которых используются оставшиеся условия задачи, составить нетрудно. Одно из них будет линейным, а другое — уравнением второй степени.

Решение системы трех уравнений рациональнее начать с решения относительно x / y полученного выше уравнения.

18.13.Стоимость автобусного билета А может быть использована только для того, чтобы определить расстояние до встречи с поездом, которое пассажиру пришлось бы проехать на такси. Эта поездка обошлась бы ему в ( А + ax − B ) p. и пройденное машиной расстояние составило бы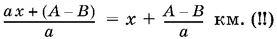

Условие задачи позволяет составить три уравнения, приравнивая различные выражения для одинаковых отрезков времени: а) время, которое заняла поездка сначала на такси, а затем на автобусе, равно времени, за которое поезд прошел тот же путь за вычетом t ; б) если бы пассажир догонял поезд на такси, то догнал бы его на расстоянии x + А — B / a км; в) остается использовать разность времен, которые входят в а) и б), и приравнять ее τ.

18.14.Условия задачи позволяют составить два уравнения, которые получатся в результате сравнения времени, за которое каждый поезд проходит весь путь без остановки, с временем, за которое поезд проходит этот же путь с остановкой и последующим увеличением скорости. (!!)

Прежде чем решать полученную систему двух уравнений с двумя неизвестными, нужно выразить через введенные неизвестные и ту величину, которая нас интересует.

18.15.Для решения задачи нам понадобятся два уравнения, которые мы получим, приравнивая промежутки времени до первой и второй встреч. Тот факт, что самолет вернулся в А , а вертолет прилетел в B , мы используем после того, как определим их скорости. Это позволит нам вычислить нужные отрезки времени для ответа на вопрос задачи.