Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

21.8.Все получившиеся после раскрытия скобок члены не будут подобными. Остается сосчитать их число.

21.9.Если n — 1 < k ≤ 2( n — 1), то члены, содержащие x k , могут быть получены лишь в результате перемножения членов суммы x k − n + 1+ ... + ... + x n — 1.

21.10.Мы приходим к неравенству 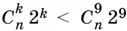, решить которое можно, придавая различные значения параметру k . B качестве таких значений удобно выбрать номера двух членов разложения, стоящих рядом с десятым членом.

21.11.Наиболее удобной является группировка

После того как мы применим формулу бинома и к (1 + x ²) k , получим, что в общем члене содержится x 100 − (5 k − 2 m ). Остается выяснить, принимает ли 5 k − 2 m все значения от 0 до 100, и если не все, то сколько значений окажутся пропущенными. Следует иметь в виду, что m , k = 0, 1, ..., 20, но m ≤ k .

21.12.Для получения рекуррентной формулы достаточно разобрать два случая: а) в первой группе один элемент ( а 1); б) в первой группе два элемента ( а 1, а 2).

21.13.Чтобы получить рекуррентную формулу, связывающую M n и M n + 1, где через M n обозначен ответ задачи, нужно найти число точек пересечения ( n + 1)-й прямой со всеми остальными. Как с этим числом связано количество вновь образовавшихся областей?

Рекуррентное соотношение будет иметь вид

M n + 1= M n + m + n + 1

22.2.После того как найдена сумма двух первых слагаемых, можно воспользоваться формулой синуса суммы, так как третье слагаемое положительно, но меньше π/ 4, и вся сумма не больше π/ 2.

22.4.Так как оба слагаемых расположены в интервале [0, π/ 2], то все тригонометрические функции от них неотрицательны.

22.5.Воспользоваться формулами приведения с тем, чтобы под знаком арккосинуса стоял косинус, а не синус.

22.9.Если перенести acrsin 3 x / 5в правую часть и взять синусы от обеих частей, то в предположении, что x > 0, получим уравнение, равносильное данному.

22.10.После взятия косинусов от обеих частей уравнения получится иррациональное уравнение, при решении которого возможно приобретение посторонних корней.

22.11.Так как обе части лежат в интервале (− π/ 2, π/ 2), то от обеих частей данного уравнения можно взять тангенсы, что не нарушит равносильности.

22.13.Ясно, что в результате взятия котангенсов от обеих частей равенства мы можем получить посторонние корни, так как у неравных углов могут быть равные котангенсы. Однако возможна и потеря корней, если в интервал изменения углов попадает значение k π.

23.6. Способ 1.B тождестве cos ( x + T )² = cos x ² удобно выбрать x = 0 и x = √2 T . Вместо второго значения можно выбрать другое иррациональное число.

Способ 2.Если у функции есть период T r , то x 1+ T = x m , x 2+ T = x k , где x i − i -й положительный корень функции. Исключив T , получим равенство, которое нужно привести к противоречию.

23.8.Предположить, что функция имеет меньший положительный период, чем наименьшее общее кратное периодов cos 3 x / 2и sin x / 3. Записать тождество и привести его к противоречию, преобразовав разность синусов и разность косинусов в произведения.

24.1.Получившийся квадратный трехчлен можно разложить на множители. Однако такой прием исследования здесь не подойдет, так как аргумент, от которого зависит квадратный трехчлен, сам является функцией от x . Используйте другой прием для исследования квадратного трехчлена.

Выделите полный квадрат.

24.2.Данную функцию удобно записать в виде разности косинусов, поскольку в аргумент каждого синуса входит 2 x — единственное слагаемое, зависящее от x .

24.3.Для этого вынести sin x cos x за скобки.

24.4. А = x + y + 1.

24.5.Найдя наименьшее значение y в каждом из пяти интервалов, мы сравним эти значения друг с другом.

24.6.Для функции y = x + а / x мы можем неравенство применить непосредственно и написать

x + a / x ≥ 2√ a .

Для данной же функции нужно иметь семь слагаемых, содержащих в знаменателе x , чтобы погасить влияние x 7. (!!)

Представить a / x в виде суммы семи одинаковых слагаемых a / 7 x .

24.8.Выразить боковую поверхность как функцию только а + b .

24.9.Удобно ввести угол α между диагональю шестиугольника и диагональю квадрата. Этот угол можно будет найти из условия, что диагонали квадрата взаимно перпендикулярны и должны принимать наибольшую возможную величину.

24.10.B условии сказано, что x — действительное число. Следовательно, дискриминант полученного квадратного уравнения не должен быть отрицательным. Это накладывает ограничения на y .

24.11.Чтобы решить систему

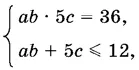
удобнее всего найти решение системы уравнений xy = 36 и x + y = 12, где x = ab , y = 5 с .

24.12.Данная функция может быть записана в виде

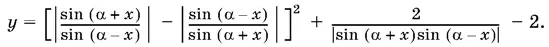
Обратите внимание на второе слагаемое. Когда оно достигает своего минимума?

24.13.Если acrsin x = α, acrcos x = β, то

α³ + β³ = (α + β) 3− 3αβ(α + β) = π³/ 8− 3π/ 2αβ.

Минимум функции достигается при α > 0 (β не может быть отрицательным), а максимум — при α < 0. Если α > 0, то появляется возможность применить оценку, в силу которой αβ ≤ ( α + β/ 2)².

24.15.После того как система приведена к виду

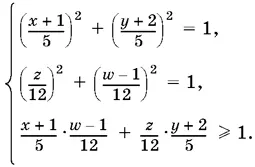
Теперь нужно ввести новые переменные. А лучше сразу обратить внимание на то, что эти переменные — синусы и косинусы двух углов. (!!)

Левая часть входящего в систему неравенства не что иное, как выражение для синуса суммы. Поэтому она не больше 1, т. е. последнее условие есть равенство. Не забудьте, что нужно найти min ( y + w ). Поэтому искать следует в области, где y < 0 и w < 0.