Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

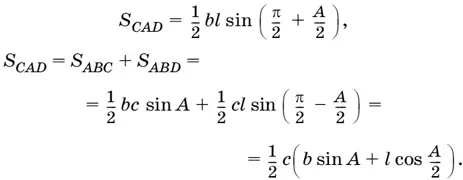
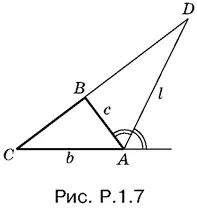
Приравнивая эти два выражения, найдем l ( b − c ) cos A / 2 = bc sin A ,

или

l ( b − c ) cos A / 2= 2 bc sin A / 2cos A / 2.

Так как cos A / 2в треугольнике не может быть равен нулю, то на него можно сократить. Теперь найдем l .

Ответ.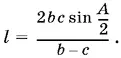

1.8.Воспользуемся сравнением площадей. С одной стороны, S = pr = a + b + c / 2 r , где через а обозначена искомая сторона. Находим отсюда, что 2 S = ar + ( b + c ) r . С другой стороны, если биссектрису угла А обозначить через l a , то

S = ½ l ab sin α/ 2+ ½ l ac sin α/ 2 = ½ l a ( b + c ) sin α/ 2

(рисунок сделайте самостоятельно). Из последнего равенства находим, что 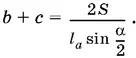Подставляем в выражение для 2 S полученное раньше:

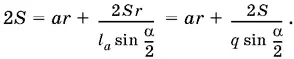
B последнем преобразовании мы учли условие задачи, согласно которому l а = rq . Осталось ввести в рассмотрение радиус R описанной окружности. По условию R = prq . По теореме синусов

a = 2 R sin α = 2 prq sin α,

откуда r = a / 2 pq sin α. Полученное соотношение позволяет определить a из последнего выражения для 2 S . B самом деле, после подстановки получим

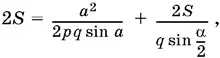
откуда после несложных преобразований найдем a .

Ответ.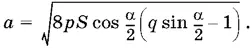

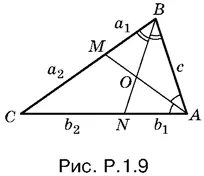
1.9.B треугольнике ABC (рис. P.1.9) введем обозначения: ВМ = a 1, СМ = a 2, АN = b 1, СN = b 2. Так как ВО — биссектриса треугольника АВМ , то AB : ВМ = АО : ОМ = √3 : 1. Аналогично AB : АN = ВО : ОN = 1 : (√3 − 1). Итак,

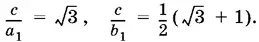
Величины a 1и b 1можно выразить через стороны треугольника

a 1= ac / b + с , b 1= bc / а + с .

После подстановки в предыдущие два равенства мы получим два однородных выражения относительно a , b и с :

b + c / a = √3, a + c / b = ½(√3 + 1),

из которых легко найти отношения a : b и с : b . Достаточно переписать эти равенства в виде

1 + с / b = √3 a / b , a / b + с / b = ½(√3 + 1).

Получим a / b = √3/ c , с / b = ½.

Таким образом, треугольник ABC подобен прямоугольному треугольнику с углами в π/ 6и π/ 3·

Ответ.Углы А , B и С равны π/ 3, π/ 2, π/ 6соответственно.

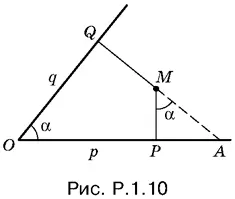
1.10.Из треугольника MPA (рис. Р.1.10) находим MP = PA ctg α. Но PA = OA − OP = q / cos α − p . Таким образом,

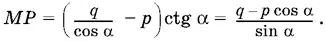
Находим MQ :

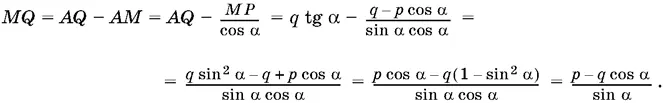
Полезно заметить, что MQ можно было не вычислять, поскольку выражение для MQ должно получиться из выражения для MP с помощью замены p на q , а q на p .

Ответ.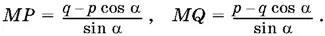

1.11.Пусть AP = 3, CR = 2√2 (рис. Р.1.11) Используя метод «сравнения площадей» для треугольника ABC, получим

3 a = 2√2 c .

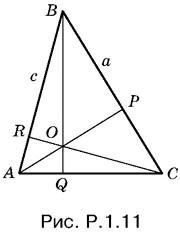
Так как а = BQ / sin C , с = BQ / sin A , то после сокращения на BQ получим

3/ sin С = 2√2/ sin А . (1)

По условию BQ = 6 OQ . Найдем отрезок AQ из треугольников ABQ и AOQ соответственно:

AQ = BQ ctg А = 6 OQ ctg А , AQ = OQ ctg ∠ OAQ ,

где ∠ OAQ = π/ 2− С . Приравнивая эти два выражения, получим второе уравнение, связывающее углы треугольника:

6 ctg А ctg С = 1. (2)

Остается решить систему из уравнений (1) и (2). Для этого возведем уравнение (1) в квадрат и воспользуемся формулой 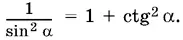Получим

9(1 + ctg² С ) = 8(1 + ctg² А ). (1′)

Из уравнения (2) следует, что

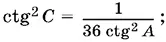
(2′)

подставляя значение ctg² С в уравнение (1'), после несложных преобразований придем к биквадратному уравнению относительно ctg А :

32 ctg 4 А − 4 ctg² А − 1 = 0. (3)

Так как треугольник ABC по условию остроугольный, то нас интересуют лишь положительные корни уравнения (3). Легко убедиться, что оно имеет единственный положительный корень ctg А = ½. Подставляя в (2), найдем ctg С = ⅓. Теперь можно найти площадь данного треугольника:

S ABC = ½ AP · a ,

где АР = 3. Величину а найдем из треугольника BRC :

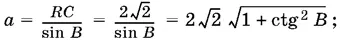
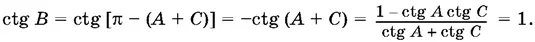
Ответ.6 см².

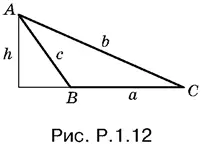
1.12.Поскольку B − С = π/ 2, угол B — тупой (рис. P.1.12).

Так как

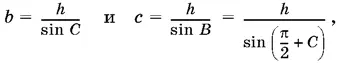
то соотношение b + с = k можно переписать так:

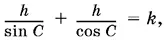
откуда

h (sin С + cos С ) = k sin С cos С .

Возведем последнее уравнение относительно sin 2 С . Корни этого уравнения