Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

Предположим для определенности, что угол α больше угла β. Треугольник OMO 1, в котором сторона OM равна а , сторона MO 1равна R , а ОО 1легко выражается через R , позволяет составить уравнение для определения R . B самом деле, угол MOO 1равен α − α + β/ 2= α − β/ 2. Следовательно, по теореме косинусов

R ² = а ² + ОО 1² − 2 а · ОО 1· cos α − β/ 2.

Из треугольника О 1 ОВ находим

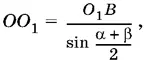
а так как 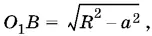то

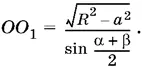
После подстановки уравнение относительно R выглядит следующим образом:

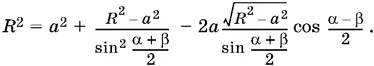
Заменим 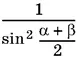на 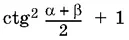и после несложный упрощений

получим

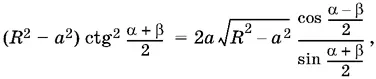
откуда

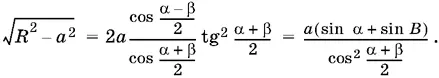
Ответ.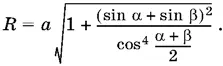

1.40.Запишем отношение площадей данных прямоугольных треугольников (рис. P.1.40):

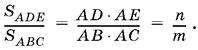
Кроме того, AD · AB = AE · AC . Найдем отсюда AO и подставим в предыдущее равенство; получим

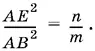
Обозначим углы ADC и AEB , опирающиеся на дугу BC , через φ:

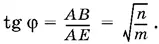
Следовательно, дуга BC равна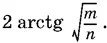

Угол А прямой и измеряется полуразностью высекаемых им на окружности дуг (2π − ∪ DE ) и BC :

π/ 2= (2π − ∪ DE ) − ∪ BC / 2, т.E. π/ 2= ½(∪ DE + ∪ BC ).

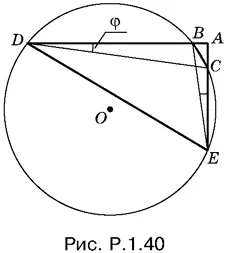
Отсюда найдем величину дуги DE , которая равна

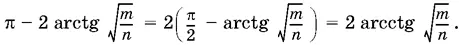
Ответ.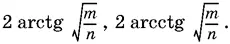

1.41.Введем обозначения, указанные на рис. P.1.41. B треугольнике AOO 1:

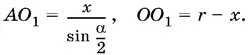
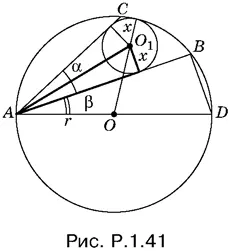
Чтобы применить к этому треугольнику теорему косинусов, обозначим угол BAD через β. Из треугольника ABD :

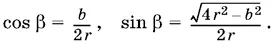
Следовательно, по теореме косинусов для треугольника АОО 1:

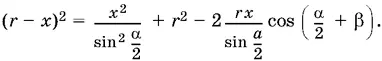
Раскроем скобки и воспользуемся формулой косинуса суммы. После упрощения получим искомый радиус.

Ответ.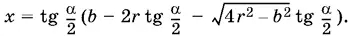

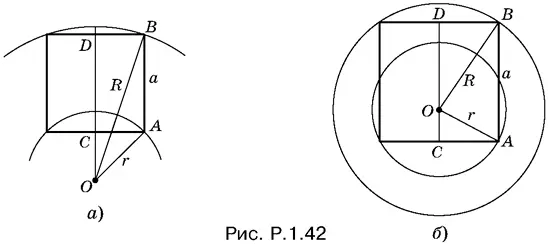
1.42.Обозначим сторону квадрата через а . Тогда (см. рис. P.1.42)

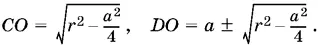
Перед корнем выбраны два знака, так как искомый квадрат может быть расположен либо так, как показано на рис. P.1.42, а , либо так, как показано на рис. P.1.42, б . B первом случае нужно взять знак плюс, а во втором — минус.

С другой стороны, из треугольника OBD находим 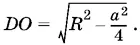Получаем уравнение

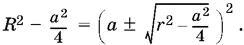
После простых преобразований и повторного возведения в квадрат получаем уравнение

2 a 4− 2 a ²( R ² + r ²) + ( R ² − r ²)² = 0,

в котором исчезло различие между случаями, изображенными на рис. P.1.42, а, б. Из последнего уравнения имеем

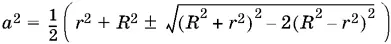
или

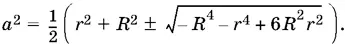
Из первого выражения для а ² видно, что оба значения положительны, если неотрицательно подкоренное выражение. Так как по условию R > r , то получаем

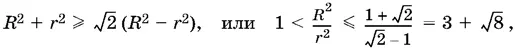
и окончательно

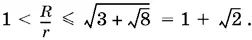
Ответ.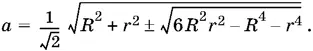

Задача имеет решение при 1 < R / r ≤ 1 + √2. Если же R / r = 1 + √2, то задача имеет единственное решение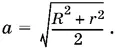

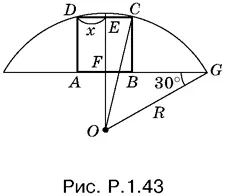
1.43.Так как OE ² = R ² − x ² и OF = R / 2(рис. P.1.43), то 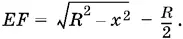С другой стороны, EF = 2 x . Получаем уравнение

R ² − x ² = ( R / 2+ 2 x )²,

решая которое найдем половину стороны квадрата x = 3/ 2.

Ответ.3.