Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

1.44.Введем обозначения, указанные на рис. P.1.44. Так как меньшая окружность вписана в угол ADC , то ее центр О 1лежит на биссектрисе этого угла.

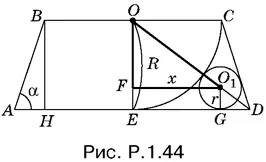
Из треугольника ОО 1 F имеем ОО ² 1= OF ² + FO ² 1, т. е.

( R + r )² = ( R − r )² + x ². (4)

Из треугольника АВН : АН = ВН ctg α = R ctg α, т. е.

а = 2 R + 2 R ctg α. (5)

Из треугольника O 1 GD :

r = ( a / 2− x )tg α/ 2. (6)

Из уравнения (4) находим 4 Rr = x ², или 2√ R √ r = x , и подставляем в уравнение (6). Получим

2 r + 4√ R √ r tg α/ 2− a tg α/ 2= 0,

или, проще,

2 ctg α/ 2 r + 4√ R √ r − a = 0.

Мы пока не будем выражать R через а и α, а, наоборот, заменим а его выражением через R и α. Это удобнее, так как квадратное уравнение таково, что впоследствии √ R можно будет вынести за скобки:

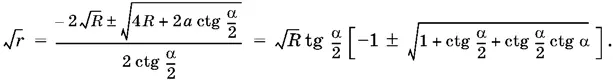
Знак минус перед корнем не имеет геометрического смысла. Если в подкоренном выражении воспользоваться формулой котангенса двойного угла, то

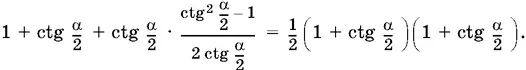
Следовательно,

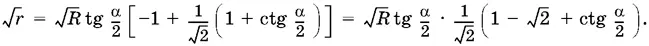
Итак,

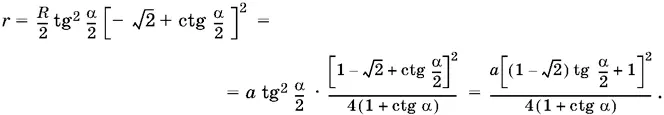
Ответ.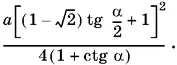

1.45.Рассмотрим вначале случай, когда диаметр CD разбивает фигуру PQNM на две части. Докажем, что фигуры CQNK и OQ 1 D равновелики (рис. P.1.45, а ). Имеем

S CKNQ = S CDQ − S KND ,

где S CDQ = S COQ + S QOD .

Итак, S CKNQ = S COQ + S QOD − S KND .

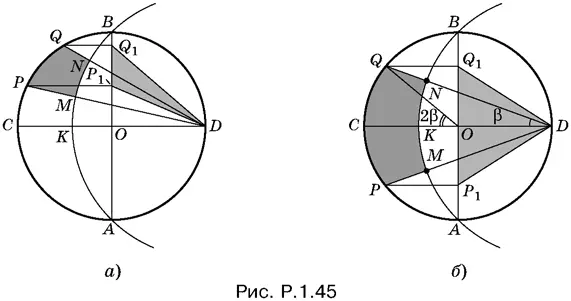
Если радиус меньшей окружности равен r , то радиус большей равен r √2. Углы CDQ и COQ опираются на общую дугу CQ , причем один из них вписан в окружность, а другой является центральным. Следовательно, если угол CDQ равен β, то угол COQ равен 2β. Теперь мы можем вычислить площади секторов COQ и KDN :

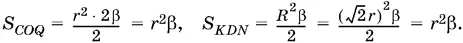
Таким образом, S COQ = S KND . Тем самым доказано, что S CKNQ = S QOD . Поскольку треугольники QOD и Q 1 OD равновелики (у них общее основание и общая высота), то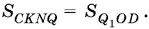

Аналогично доказывается равенство 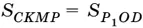, что и завершает доказательство для случая, когда точки P и Q лежат по разные стороны от CD .

Если точки P и Q лежат по одну сторону от диаметра (рис. P.1.45, б ), то решение не меняется. Только в конце найденные площади придется не складывать, а вычитать.

1.46.Из треугольника OAK (рис. P.1.46)

OK ² = R ² − ( AB / 2)².

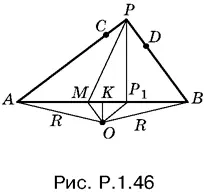
Так как KP 1= AP 1− AB / 2, то из треугольника OKP 1

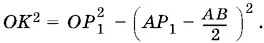
По условию OP 1= MP 1. Приравнивая два полученных выражения для OK ² и заменяя ОР 1на МР 1, найдем

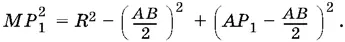
Нам нужно вычислить длину отрезка MP . Чтобы воспользоваться прямоугольным треугольником MPP 1, в котором мы знаем длину МР 1, нужно вычислить PP 1. Так как треугольник APB прямоугольный, то 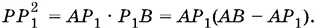Теперь можно вычислить и МР :

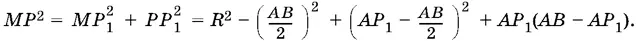
Раскрывая скобки и приводя подобные члены, получим MP ² = R ².

Ответ. R .

1.47.Из треугольника AOC (рис. P.1.47) легко найти AC = 4 R / 5. Так как AC · СВ = МС · CN , то

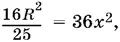
откуда x = 2 R / 15.

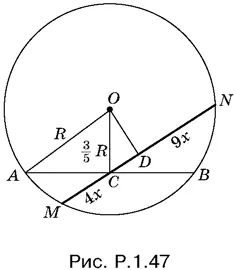
Проведем перпендикуляр OD к хорде MN . Так как MD = 13 x / 2, то

CD = MD − МС = 5 x / 2= R / 3.

Косинус угла OCD равен синусу искомого угла NCB :

CD / OC = R / 3 : 3 R / 5= 5/ 9.

Ответ.arcsin 5/ 9.

1.48.Соединим центры О 2и O 1рассматриваемых окружностей. Отрезок O 1 О 2 равен x + R / 2(рис. P.1.48).

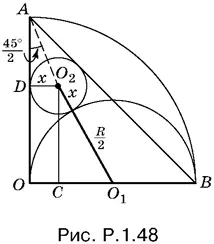
Центр О 2лежит на биссектрисе угла OAB , равного 45°. Поэтому угол DAO 2равен 45°/ 2. Это позволяет выразить через R и x отрезок DO :

DO = R − AD = R − x ctg 45°/ 2= R − x 1 + cos 45°/ sin 45°= R − x (√2 + 1).

Так как CO 1= R / 2− x , O 2 С = DO = R − x (√2 + 1), а O 1 O 2= x + R / 2, то по теореме Пифагора для треугольника O 2 CO 1получим

( R / 2− x )² + [ R − x (√2 + 1)]² = ( R / 2 + x )²,

или после преобразований

[ R − x (√2 + 1)]² = 2 Rx ,

т. е.

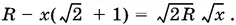
Получили квадратное уравнение относительно √ x . Решая его, найдем

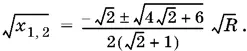
Так как 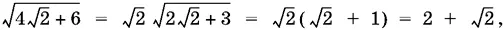то

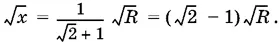(Второе значение √ x не имеет смысла.)

Ответ. x = (3 − 2√2) R .

1.49.Соединим точки M и C (рис. P.1.49).