Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

2.15.Так как дуга AmB фиксирована, то известен и вписанный угол АМВ . Обозначим его через φ. Если отрезок PQ (рис. P.2.15) перенести параллельно в отрезок В 1 В , то из точки P отрезок АВ 1будет виден под углом φ. Таким образом, строим отрезок В 1 В , равный а и параллельный CD ; на отрезке АВ 1строим сегмент, вмещающий угол φ, где φ — угол, измеряемый дугой AmB данной окружности. Искомая точка P есть точка пересечения или касания дуги этого сегмента с прямой CD .

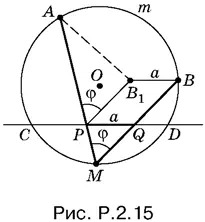
Задача может иметь два решения (сегмент, опирающийся на АВ 1, пересекает хорду CD ), одно решение (этот сегмент касается хорды) и может не иметь решений вовсе (точек пересечения нет).

2.16.Пусть отрезок FD делится точкой M пополам (рис. P.2.16). Отразим точку B от точки M . Получим точку E . Отрезки FD и ЕВ можно рассматривать как диагонали параллелограмма.

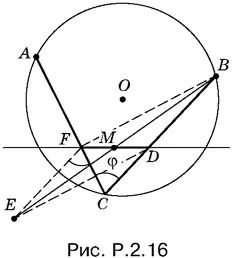
Заметим также, что угол АСВ известен, так как точки А и B зафиксированы на окружности; обозначим его через φ. Угол АFЕ равен π − φ. Следовательно, точка F обладает еще и тем свойством, что из нее отрезок AE виден под данным углом π − φ.

Итак, строим точку E , а на отрезке AE — сегмент, вмещающий угол π − φ. На пересечении дуги этого сегмента с данной прямой получим точку F .

Задача имеет единственное решение, если точки А и B лежат по одну сторону от данной прямой, и не имеет решений в остальных случаях.

2.17.Пусть прямая, проведенная через точки А и B , пересекает прямую PQ в точке С (рис. P.2.17), и пусть О — центр искомой окружности. Тогда СА · СВ = CD ². Отрезки СА и СВ известны, отрезок CD — их среднее геометрическое и строится стандартным образом.

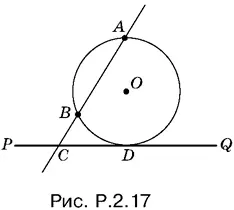
Если точки А и B лежат по одну сторону от PQ , то задача имеет два решения (отрезок CD можно отложить вправо и влево от точки С). Если AB и PQ параллельны, то задача имеет единственное решение, которое очевидно, но не может быть получено описанным способом. Когда точки А и P лежат по разные стороны PQ , задача не имеет решения.

2.18.Отрезки МВ и МА или их продолжения пересекают данную окружность в точках С и D (рис. P.2.18), которые являются основаниями высот треугольника АМВ , опущенных из его вершин А и B. Отрезок МР , проведенный через точку P пересечения AC и BD , будет искомым перпендикуляром.

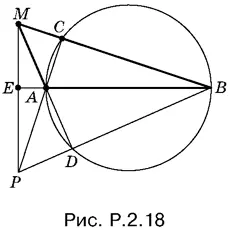
Задача имеет решение, если точка M не лежит на прямой AB.

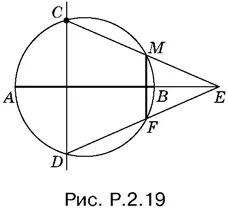
2.19.Предыдущая задача позволяет построить некоторый перпендикуляр к диаметру AB , пересекающий данную окружность в точках, которые мы обозначим буквами С и D (рис. P.2.19). Проведем прямую СМ ; она пересечет диаметр AB (или его продолжение) в точке E . Проведем ED . B пересечении ED и данной окружности получим точку F ; MF — искомый перпендикуляр.

2.20.Построим точку А 1симметричную точке А относительно прямой l (рис. P.2.20). Для любой точки С на прямой l (в силу неравенства треугольника) справедливо соотношение

| AC − BC | = | А 1 С − BC | ≤ А 1 В .

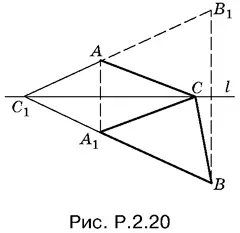
Величина | А 1 С − BC | будет меняться в зависимости от положения точки С , и станет наибольшей, когда точка С займет положение С 1(на пересечении прямых А 1 B и l ). Именно для этой точки треугольник СА 1 В вырождается в отрезок С 1 В , а неравенство треугольника превращается в равенство: | А 1 С − BC | = А 1 B . Из построения следует, что точка С единственная (если бы мы отражали от прямой l точку B , то пришли бы к той же точке С ).

2.21.Две противоположные вершины искомого квадрата лежат, во-первых, на внешних полуокружностях, построенных на сторонах данного четырехугольника (рис. P.2.21), и, во-вторых, на диагонали квадрата, которая пересекает внутренние полуокружности в точках E и F , таких, что АF = FB = DE = EC = 45°.

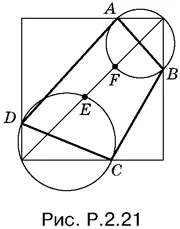
После проведенного анализа построение очевидно.

2.22.Выберем на глаз отрезок длины 1. Построим прямоугольный треугольник с катетами 1 и 1. Гипотенуза его равна √2. Далее возьмем катеты 1 и √2. Получим гипотенузу √3. Если же катеты равны √3 и 2, то гипотенуза равна √7. На сторонах острого угла А (для удобства) отложим AB = 1, АВ 1= √7, AC = √7 (рис. P.2.22).

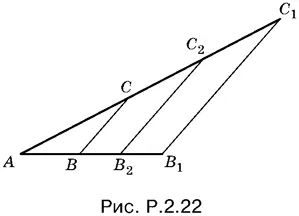
Соединим B и С , через В 1проведем прямую, параллельную BC . Она пересечет AC в точке С 1. Из подобия треугольников ABC и АВ 1 С 1имеем AB : АВ 1= AC : АС 1. Отсюда 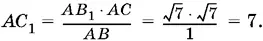Однако это 7 выбранных нами единиц, а не реальный отрезок длины 7, данный в условии задачи. Отложим АС 2= 7. Это уже данный в условии отрезок. И проведем С 2 В 2|| СВ. Отрезок АВ 2= √7.

2.23.Так как длина искомого отрезка есть

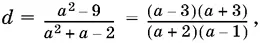
а длина данного отрезка равна а , то рассмотрим только такие значения а , что одновременно

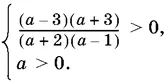
Решение этой системы есть два интервала: 0 < а < 1 и а > 3.

Пусть 0 < а < 1. Тогда удобнее записать длину искомого отрезка так:

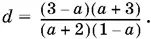
На одном луче угла отложим отрезки OA = 2 + а и OB = 3 + а, а на другом луче — отрезок ОС = 3 − а (рис. P.2.23, а ). Соединим А и С , проведем BD || AC. Тогда