Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

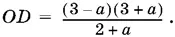
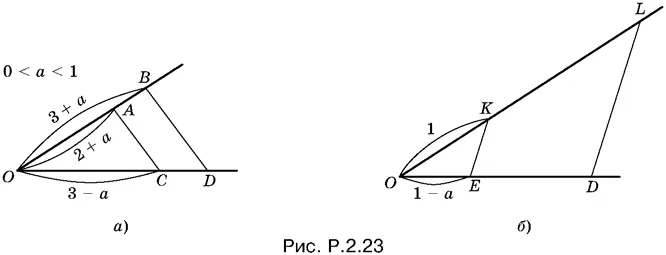
Осталось построить отрезок, длина которого равна OD / 1 − а . Для этого отложим на одном луче угла отрезки OD и ОЕ = 1 − а, а на другом луче отрезок OK = 1 (рис. P.2.23, б). Проведем DL || EK . Отрезок OL имеет искомую длину:

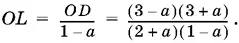
Осталось рассмотреть случай а > 3. Решение отличается только тем, что вместо отрезков длины 3 − а и 1 − а придется рассматривать отрезки длины а − 3 и а − 1.

3.1.На луче, перпендикулярном к MN , возьмем произвольную точку А (рис. P.3.1). Спроецируем OA на плоскость P , а полученный отрезок OB на второй из данных лучей. Треугольник АСО прямоугольный (по теореме о трех перпендикулярах).

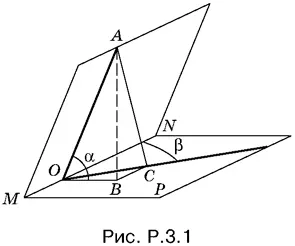
Косинус искомого угла АОС равен ОС / OA . Используя построенным треугольники, можно выразить ОС через OA :

ОС = OB sin β = OA cos α sin β.

Ответ.arccos (cos α sin β).

3.2.Спроецируем данный треугольник ABC на плоскость P (рис. P.3.2) и построим угол CED , равный x , между плоскостью треугольника и плоскостью P . Введем в рассмотрение линейный элемент CD = а .

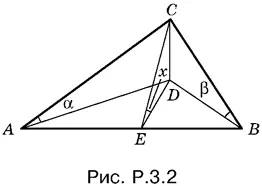
Тогда

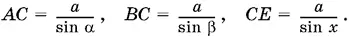
Так как СЕ — высота в треугольнике ABC , опущенная на гипотенузу, то (из сравнения площадей) имеем

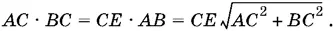
Подставляя вычисленные раньше значения AC , BC и СЕ, получим

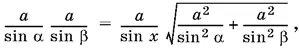
откуда

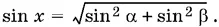
Так как угол x по построению всегда острый, то он определяется однозначно.

Ответ.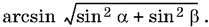

3.3.Из некоторой точки В 1на стороне угла α опустим перпендикуляр B 1 B на плоскость P (рис. P.3.3). Через В 1проведем плоскость, параллельную плоскости P . Она пересечет другую сторону угла α в некоторой точке А 1. Через B 1 B и А проведем плоскость, которая будет перпендикулярна к плоскости P .

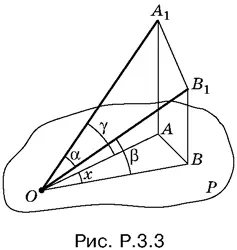
Отрезки AA 1и ВВ 1равны. Обозначим АА 1= ВВ 1= а . Теперь можно вычислить все стороны треугольника ОАВ и воспользоваться теоремой косинусов, чтобы найти угол x .

Стороны OA и OB вычислить просто:

OA = а ctg γ, OB = а ctg β.

Сторона AB равна А 1 В 1в треугольнике ОА 1 В 1. Так как

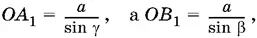
то по теореме косинусов

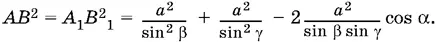
Воспользуемся теоремой косинусов еще раз, но уже для треугольника ОАВ :

АВ ² = ОА ² + ОВ ² − 2 ОА · OB cos x .

Подставляя сюда найденные выше выражения для OA , OB и AB , получим уравнение относительно cos x . Решая его, после несложных тригонометрических преобразований найдем cos x .

Ответ.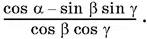

3.4.Построим плоскость P , перпендикулярную к прямой а , и спроецируем на нее прямые b , с и d . Искомая прямая параллельна а , т. е. должна спроецироваться в точку О на плоскости P . Точка О будет одинаково удалена от проекций b 1, с 1и d 1трех этих прямых.

Поскольку прямые а , b , с и d скрещивающиеся, ни одна из прямых b , с и d не может спроецироваться в точку на плоскости P , так как иначе она оказалась бы параллельной прямой а .

Проекции никаких двух прямых из b , с , d не сольются, так как это означало бы, что эти две прямые лежат в одной плоскости. Поэтому проекции b 1, с 1и d 1могут расположиться на плоскости P лишь одним из четырех способов (рис. P.3.4, а ).

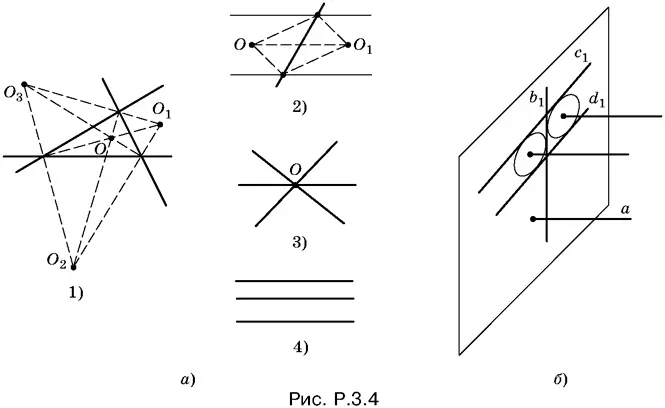
B первом случае (проекции образуют треугольник) мы получим четыре точки, равноотстоящие от b 1, с 1и d 1. Это — центры вписанной и вневписанных окружностей. Проводя через каждую из них прямую, перпендикулярную к плоскости P , придем к четырем решениям.

Во втором случае (две из проекций параллельны) получим два решения (рис. P.3.4, б ).

B третьем случае (проекции пересекаются в одной точке) будет единственное решение — прямая, проходящая через общую для трех проекций точку.

B последнем случае (проекции b 1, с 1и d 1 параллельны) решения нет.

Так как все возможные случаи исчерпаны, то задача решена.

3.5.Проведем CD параллельно AB (рис. P.3.5).

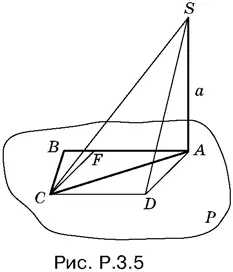
Угол SCD искомый. Построим CF ⊥ AB и AD ⊥ AB . B прямоугольнике AFCD имеем CD = АF = а / 2, AD = CF = . Из треугольника SAD находим 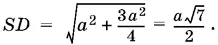Тангенс угла SCD равен SD : CD .

Ответ.√7.

3.6.Если OK = ½ AB = OA , то треугольники OAM и OKM (рис. P.3.6) равны. Таким образом, условие OK = OA равносильно условию AM = KM и (совершенно аналогично) условию BP = KP .

Отрезок OK входит в оба треугольника OKM и OKP :