Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

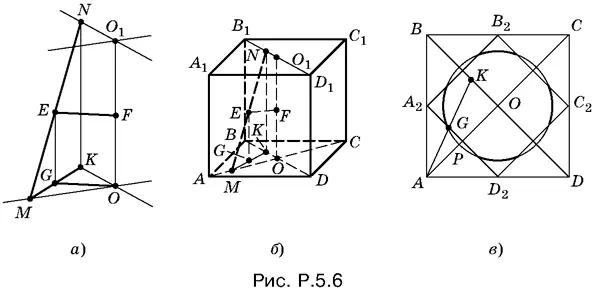
Итак, если точка E принадлежит искомому геометрическому месту, то она лежит в плоскости, параллельной основаниям куба и проходящей через середину F отрезка OO 1, и принадлежит окружности радиусом 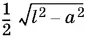с центром в точке F .

Для той измененной задачи, которую мы рассматриваем, верно и обратное утверждение: любую точку E , принадлежащую описанной выше окружности, можно спроецировать в точку G плоскости нижнего основания и радиусом GO сделать из точки G засечки M и K на диагональных прямых нижнего основания. Построив перпендикуляр NK , мы сможем найти и отрезок МN длины l , серединой которого является точка E .

Теперь остается учесть тот факт, что точка E и отрезок МN не должны покидать пределы куба.

Для этого нужно уловить тот момент, после которого один конец отрезка MN , например M , покинет куб. Ясно, что это произойдет, когда точка M совместится с одной из вершин квадрата ABCD . Пусть точка M совпала с вершиной А (рис. P.5.6, б ). B зависимости от длины l отрезка МN проекция K точки N расположится на отрезке OB . При изменении длины отрезка МN точка K пробегает весь отрезок BO , а середина G отрезка MK пробегает в это время отрезок А 2 Р , являющийся средней линией треугольника АВO .

Теперь ясно, что проекция точки E на плоскость нижнего основания куба не может выйти из квадрата А 2 В 2 С 2 D 2(рис. P.5.6, в ).

Итак, искомое геометрическое место точек расположено в горизонтальном сечении куба, проходящем через его центр. Это — часть окружности с центром в центре куба, не выходящая за пределы квадрата, проецирующегося в А 2 В 2 С 2 D 2.

6.1.Имеем p ² − 1 = ( p − 1)( p + 1), а p − 1, p , p + 1 − три последовательных числа, из которых p > 3 простое. Следовательно, p − 1 и p + 1 — два последовательных четных числа, т. е. одно из них обязательно делится на четыре, а произведение делится на восемь. Известно, что из трех последовательных целых чисел одно делится на три. Но p — простое, следовательно, на три делится либо p − 1, либо p + 1. Мы доказали, что p ² − 1 делится на 8 · 3 = 24.

6.2. Способ 1.Предположим, что n ³ + 2 n делится на 3 при n = k . (Если n = 1, то это очевидно.) Тогда при n = k + 1 получим

( k + 1)³ + 2( k + 1) = k ³ + 3 k ² + 3 k + 1 + (2 k + 2) = ( k ³ + 2 k ) + 3 k ² + 3 k + 3.

Так как k ³ + 2 k делится на 3, то и ( k + 1)³ + 2( k + 1) тоже делится на 3. B силу принципа индукции утверждение доказано.

Способ 2.Так как n ³ + 2 n = n ( n ² + 2), то при n = 3 k делимость на 3 очевидна. Если же n = 3 k ± 1, то n ² + 2 = (3 k ± 1)² + 2 = 9 k ² ± 6 k + 3 и также делится на 3.

6.3.Разложим данное число на множители двумя способами:

3 105+ 4 105= (3 5) 21+ (4 5) 21= 243 21+ 1024 21= (243 + 1024)(243 20− ... + 1024 20) = 181 · 7(243 20− ... + 1024 20);

3 105+ 4 105= (3 7) 15+ (4 7) 15= 2187 15+ 16 384 15= (2187 + 16 384)(2187 14− ... + 16 384 14) = 18 571(2187 14− ... + 16 384 14) = 49 · 379(2187 14− ... + 16 384 14).

Таким образом, данное число делится на 49 и на 181.

6.4.Множитель 2 содержится не менее одного раза во всех четных числах, не менее двух раз во всех числах, делящихся на 4, не менее трех раз в числах, делящихся на 8, и т. д. Поэтому четные числа мы должны сосчитать отдельно, прибавить к ним количество чисел, делящихся на 4, к ним прибавить количество чисел, делящихся на 8, и т. д. B результате получим

250 + 125 + 62 + 31 + 15 + 7 + 3 + 1 = 494.

B этой сумме каждое следующее слагаемое получено из предыдущего как целая часть от деления его на два.

Ответ.494.

6.5.Если умножить данное число на 10, то его свойство быть кратным 81 не изменится. Получим число

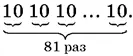
Сумма цифр этого числа делится на 9. Разобьем его на 9 одинаковых секций

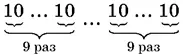
и будем делить на 9. Так как сумма цифр в каждой секции равна 9, то каждая секция делится на 9. Обозначим частное от деления одной секции на 9 через А . B результате деления на 9 всего числа получим частное

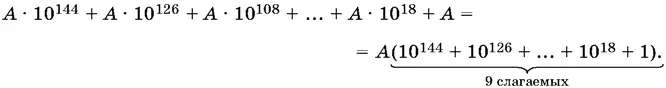
Сумма цифр числа, стоящего в скобках, равна 9. Следовательно, полученное частное делится на 9, а данное число — на 81.

6.6.Дополним n 4+ 4 до полного квадрата:

n 4+ 4 n ² + 4 − 4 n ² = ( n ² + 2)² − 4 n ² = ( n ² − 2 n + 2)( n ² + 2 n + 2).

Число n 4+ 4 может быть простым только в том случае, если либо n ² − 2 n + 2 = 1, либо n ² + 2 n + 2 = 1. Решая эти уравнения, получим n = 1, n = −1. При n = ±1 данное выражение равно 5, т. е. является простым числом.

Ответ. n = ±1.

6.7.Подставим n = 2 k , получим

n / 12+ n ²/ 8+ n ³/ 24= k / 6+ k ²/ 2+ k ³/ 3= 2 k ³ + 3 k ² + k / 6= k ( k + 1)(2 k + 1)/ 6.

Остается доказать, что числитель всегда делится на 6.

Так как одно из двух последовательных целых чисел k и k + 1 четное, то делимость на 2 очевидна. Если ни k , ни k + 1 не делятся на 3, то k = 3 m + 1, а k + 1 = 3 m + 2. Тогда 2 k + 1 = 2(3 m + 1) + 1 = 6 m + 3, т. е. 2 k + 1 делится на 3. Тем самым доказательство закончено.

6.8. Способ 1.Если дробь сократима, то

5 x + 7 = qr , 2 x + 3 = pr .

Исключая из этих равенств x , получим

1 = (5 p − 2 q ) r , или 1/ r = 5 p − 2 q .

Если дробь 2 x + 3/ 5 x + 7сократима на целое число r ≠ ±1, то в последнем равенстве справа стоит целое число, а слева — не целое. Таким образом, это равенство противоречиво, и данная дробь не сократима.

Способ 2.Если данная дробь сократима, то сократима и дробь

5 x + 7/ 2 x + 3 = 2 + x + 1/ 2 x + 3.

Таким образом, должна быть сократимой дробь, стоящая в правой части и, следовательно, дробь

2 x + 3/ x + 1= 2 + 1/ x + 1.

Дробь 1/ x + 1не сократима ни при каких x , так как в числителе стоит единица.

Итак, данная дробь не сократима ни при каких x .